Wheels
When modeling wheels, there are several different assumptions that can be made, such as
- Is the wheel able to leave the ground or not?
- Can the wheel slip or does it roll perfectly?
The wheel-related components available are
RollingWheel: a wheel that can roll on the ground. It cannot slip and it cannot leave the ground.RollingWheelJoint: a lower-level component used inRollingWheelto model the kinematics of the wheel, without inertial or mass properties.SlipWheel: SimilarRollingWheel, but can also slip.SlipWheelJoint: Similar toRollingWheelJoint, but forSlipWheel.RollingWheelSet: a set of two wheels connected by an axis. One of the wheels cannot slip, while the other one slips as required to allow the wheel set to turn (no differential is modeled). No wheel can leave the ground.RollingWheelSetJoint: A lower-level component used inRollingWheelSetto model the kinematics of the wheel set, without inertial or mass properties.RollingConstraintVerticalWheel: A low-level constraint that is used to enforce a perfectly rolling wheel that is always vertical, i.e., it can only roll forward and not fall down.PlanarMechanics.SimpleWheel: A 2D wheel component with a simple, linear lateral slip model.PlanarMechanics.SlipBasedWheelJoint: A more advanced 2D wheel component with slip-dependent friction characteristics.
All wheel components are limited to rolling on the $xz$ plane, i.e., the gravity direction must be the default [0, -1, 0].
Rolling wheel
using Multibody
using ModelingToolkit
import ModelingToolkitStandardLibrary.Mechanical.Rotational
import ModelingToolkitStandardLibrary.Blocks
using Plots
using OrdinaryDiffEq
using LinearAlgebra
using JuliaSimCompiler
using Test
t = Multibody.t
D = Differential(t)
@mtkmodel WheelInWorld begin
@components begin
world = World()
wheel = RollingWheel(
radius = 0.3,
m = 2,
I_axis = 0.06,
I_long = 0.12,
x0 = 0.2,
z0 = 0.2,
der_angles = [0, 5, 1],
)
end
end
@named worldwheel = WheelInWorld()
worldwheel = complete(worldwheel)
defs = Dict([
worldwheel.wheel.body.r_0[1] => 0.2;
worldwheel.wheel.body.r_0[2] => 0.3;
worldwheel.wheel.body.r_0[3] => 0.2;
])
ssys = structural_simplify(multibody(worldwheel))
prob = ODEProblem(ssys, defs, (0, 4))
sol = solve(prob, Tsit5())
@test SciMLBase.successful_retcode(sol)Test Passedimport GLMakie
Multibody.render(worldwheel, sol; filename = "worldwheel.gif")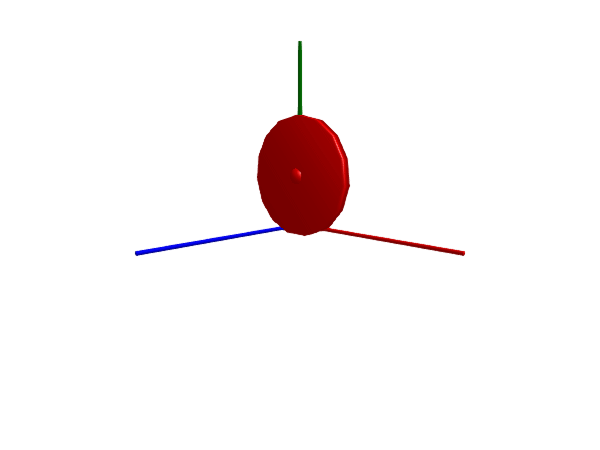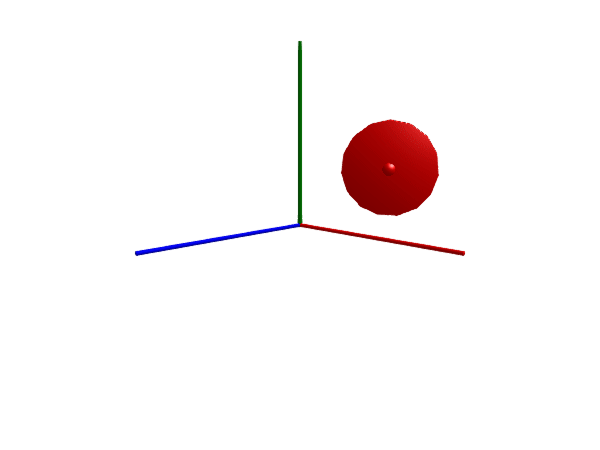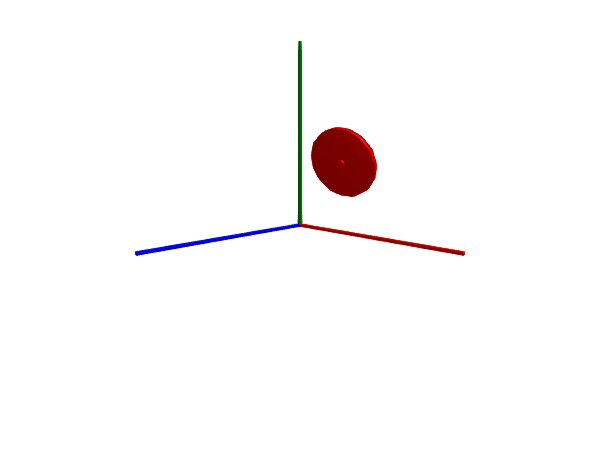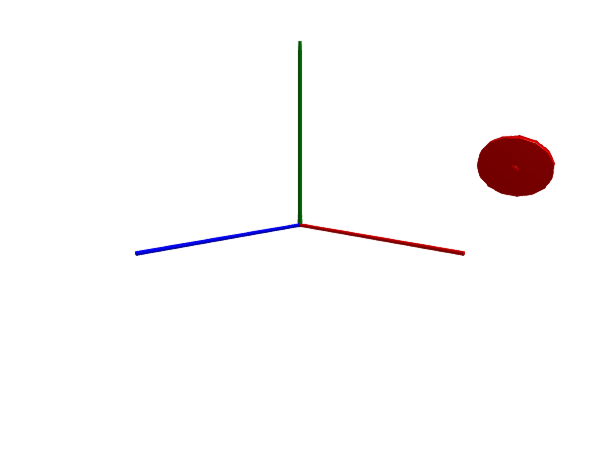
Add slip
The example below is similar to that above, but models a wheel with slip properties instead of ideal rolling. We start by showing the slip model
using Plots
vAdhesion = 0.2
vSlide = 0.4
mu_A = 0.95
mu_S = 0.7
v = range(0, stop=1, length=500) # Simulating the slip velocity
μ = Multibody.PlanarMechanics.limit_S_triple.(vAdhesion, vSlide, mu_A, mu_S, v)
plot(v, μ, label=nothing, lw=2, color=:black, xlabel = "\$v_{Slip}\$", ylabel = "\$\\mu\$")
scatter!([vAdhesion, vSlide], [mu_A, mu_S], color=:white, markerstrokecolor=:black)
hline!([mu_A, mu_S], linestyle=:dash, color=:black, alpha=0.5)
vline!([vAdhesion, vSlide], linestyle=:dash, color=:black, alpha=0.5)
plot!(
xticks = ((vAdhesion, vSlide), ["\$v_{Adhesion}\$", "\$v_{Slide}\$"]),
yticks = ((mu_A, mu_S), ["\$\\mu_{adhesion}\$", "\$\\mu_{slide}\$"]),
framestyle = :zerolines,
legend = false,
)The longitudinal force on the tire is given by
\[f_{long} = - f_n \dfrac{\mu(v_{Slip})}{v_{Slip}} v_{SlipLong}\]
where f_n is the normal force on the tire, μ is the friction coefficient from the slip model, and v_{Slip} is the magnitude of the slip velocity.
The slip velocity is defined such that when the wheel is moving with positive velocity and increasing in speed (accelerating), the slip velocity is negative, i.e., the contact patch is moving slightly backwards. When the wheel is moving with positive velocity and decreasing in speed (braking), the slip velocity is positive, i.e., the contact patch is moving slightly forwards.
@mtkmodel SlipWheelInWorld begin
@components begin
world = World()
wheel = SlippingWheel(
radius = 0.3,
m = 2,
I_axis = 0.06,
I_long = 0.12,
x0 = 0.2,
z0 = 0.2,
der_angles = [0, 25, 0.1],
mu_A = 0.95, # Friction coefficient at adhesion
mu_S = 0.5, # Friction coefficient at sliding
sAdhesion = 0.04, # Adhesion slippage
sSlide = 0.12, # Sliding slippage
vAdhesion_min = 0.05, # Minimum adhesion velocity
vSlide_min = 0.15, # Minimum sliding velocity
)
end
end
@named worldwheel = SlipWheelInWorld()
worldwheel = complete(worldwheel)
defs = Dict([
worldwheel.wheel.body.r_0[1] => 0.2;
worldwheel.wheel.body.r_0[2] => 0.3;
worldwheel.wheel.body.r_0[3] => 0.2;
worldwheel.wheel.frame_a.render => true;
worldwheel.wheel.frame_a.length => 0.4;
worldwheel.wheel.frame_a.radius => 0.01;
])
ssys = structural_simplify(multibody(worldwheel))
prob = ODEProblem(ssys, defs, (0, 3))
sol = solve(prob, Tsit5())
@test SciMLBase.successful_retcode(sol)Test PassedMultibody.render(worldwheel, sol; filename = "slipping_worldwheel.gif", x=4, z=2, time_scale=3)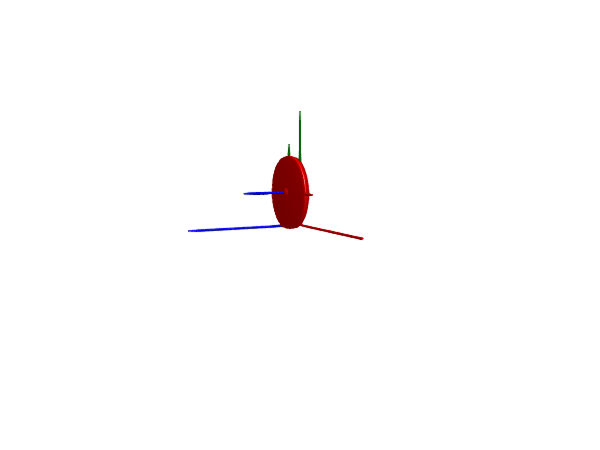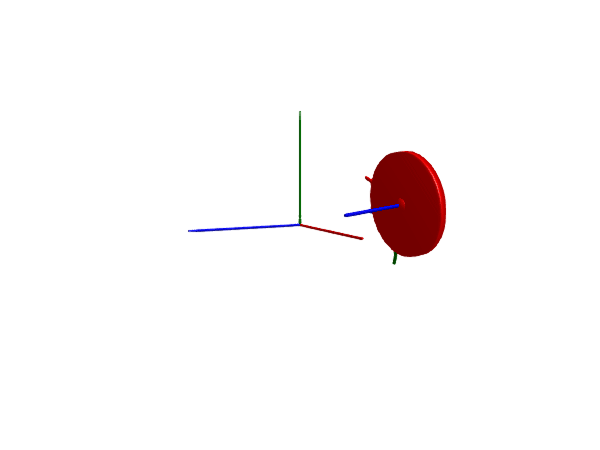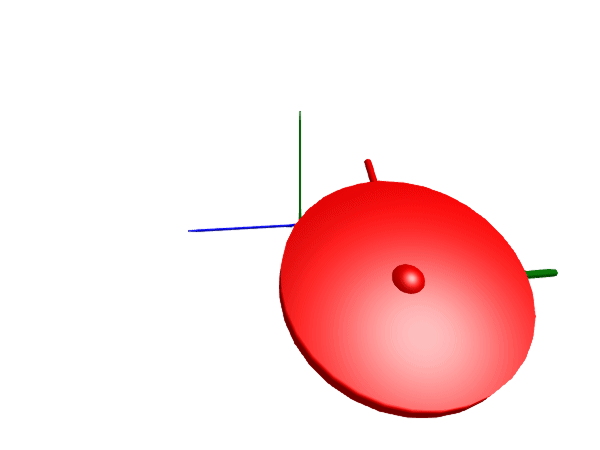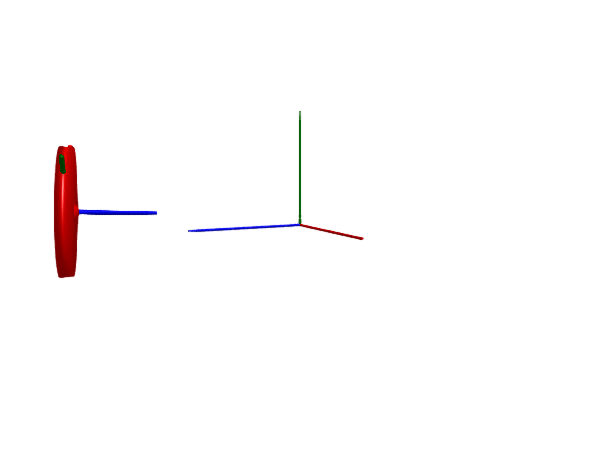
Notice how the wheel starts out with zero linear velocity but large rotational velocity, causing it to initially slip before picking up speed and gaining traction.
In this animation, we render also the connector frame of the wheel to make it easier to see that the wheel is spinning.
Wheel set
A RollingWheelSet is comprised out of two wheels mounted on a common axis through their axis of rotation.
@mtkmodel DrivingWheelSet begin
@components begin
sine1 = Blocks.Sine(frequency=1, amplitude=2)
sine2 = Blocks.Sine(frequency=1, amplitude=2, phase=pi/2)
torque1 = Rotational.Torque()
torque2 = Rotational.Torque()
wheels = RollingWheelSet(radius=0.1, m_wheel=0.5, I_axis=0.01, I_long=0.02, track=0.5, state_priority=100)
bar = FixedTranslation(r = [0.2, 0, 0])
body = Body(m=0.01, state_priority=1)
world = World()
end
@equations begin
connect(sine1.output, torque1.tau)
connect(sine2.output, torque2.tau)
connect(torque1.flange, wheels.axis1)
connect(torque2.flange, wheels.axis2)
connect(wheels.frame_middle, bar.frame_a)
connect(bar.frame_b, body.frame_a)
end
end
@named model = DrivingWheelSet()
model = complete(model)
ssys = structural_simplify(multibody(model))
# display(unknowns(ssys))
prob = ODEProblem(ssys, [
model.wheels.wheelSetJoint.prismatic1.s => 0.1
model.wheels.wheelSetJoint.prismatic2.s => 0.1
], (0, 3))
sol = solve(prob, Tsit5())
@test SciMLBase.successful_retcode(sol)Test Passedimport GLMakie
Multibody.render(model, sol; filename = "wheelset.gif")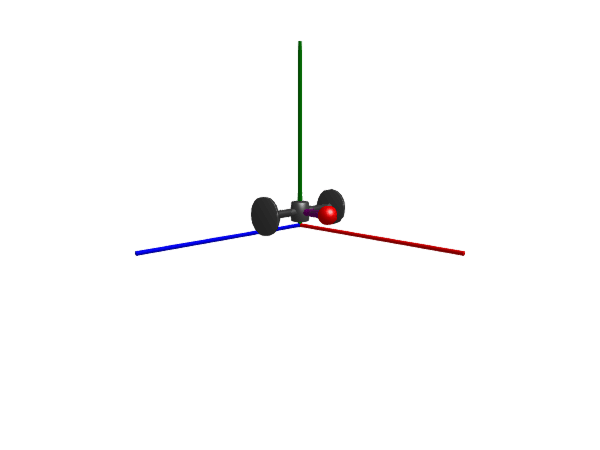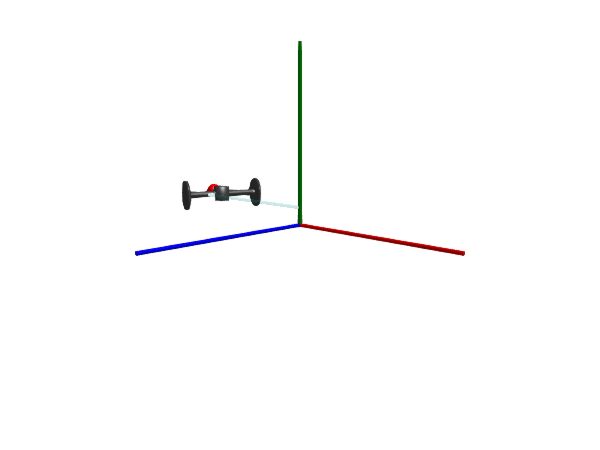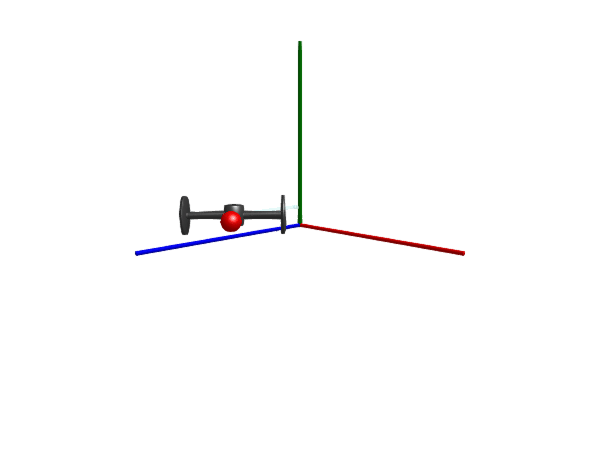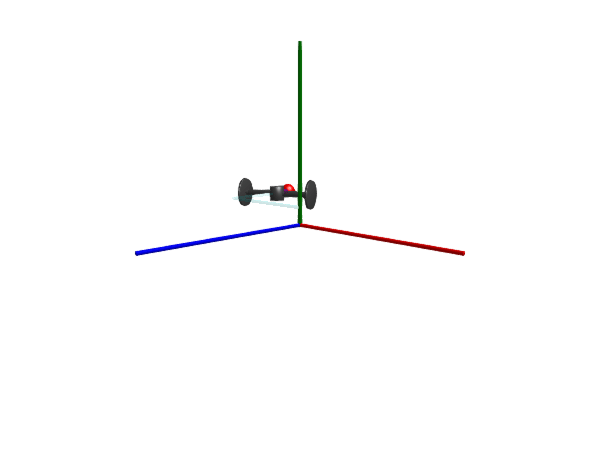
The RollingWheelSet includes constraints that prevent the wheels from leaving the ground and the connector frame_middle from rotating around the wheel axis. This means that if two wheel sets are connected to the same body, the system will be over constrained. To solve this, pass iscut = true to one of the wheel sets, like below:
wheel_mass = 15
I_axis=0.01
I_long=0.02
wheel_d = 2
wheel_radius = 0.25
tire_black = [0.1, 0.1, 0.1, 1]
@mtkmodel Car begin
@structural_parameters begin
l=4
m=108
end
@parameters begin
I=10
g=0
end
@components begin
world = World()
sine1 = Blocks.Sine(frequency=1, amplitude=150)
sine2 = Blocks.Sine(frequency=1, amplitude=150, phase=pi/6)
torque1 = Rotational.Torque()
torque2 = Rotational.Torque()
front_wheels = RollingWheelSet(radius=wheel_radius, m_wheel=wheel_mass, I_axis, I_long, track=wheel_d)
rear_wheels = RollingWheelSet(radius=wheel_radius, m_wheel=wheel_mass, I_axis, I_long, track=wheel_d, iscut=true)
steering_joint = Revolute(n = [0,1,0], axisflange=true, state_priority=100)
prefer_straight_ahead = Rotational.SpringDamper(d=10, c=10)
body = BodyShape(; m, r = [l, 0, 0], I_22 = I, radius=0.3)
end
@equations begin
connect(sine1.output, torque1.tau)
connect(sine2.output, torque2.tau)
connect(torque1.flange, front_wheels.axis1)
connect(torque2.flange, front_wheels.axis2)
connect(front_wheels.frame_middle, steering_joint.frame_a)
connect(steering_joint.frame_b, body.frame_a)
connect(rear_wheels.frame_middle, body.frame_b)
connect(prefer_straight_ahead.flange_a, steering_joint.axis)
connect(prefer_straight_ahead.flange_b, steering_joint.support)
end
end
@named model = Car()
model = complete(model)
ssys = structural_simplify(multibody(model))
prob = ODEProblem(ssys, [], (0, 6))
sol = solve(prob, Tsit5())
render(model, sol, framerate=30, filename="car.gif", x=6, z=6, y=5)
Simple planar wheel
This example demonstrates how we can model a simple single-track vehicle with planar (2D or 3DOF) components.
We will use the component PlanarMechanics.SimpleWheel, together with a PlanarMechanics.Revolute joint to connect the front wheel to the PlanarMechanics.BodyShape representing the vehicle body. The revolute joint is used for steering.
import Multibody.PlanarMechanics as Pl
@mtkmodel TestWheel begin
@components begin
body = Pl.BodyShape(r = [1.0, 0.0], m=1, I=0.1, gy=0)
revolute = Pl.Revolute()
wheel1 = Pl.SimpleWheel(color=tire_black)
wheel2 = Pl.SimpleWheel(color=tire_black, μ=.5)
thrust_input1 = Blocks.Constant(k=1)
thrust_input2 = Blocks.Constant(k=0)
end
@equations begin
connect(body.frame_a, revolute.frame_a)
connect(revolute.frame_b, wheel1.frame_a)
connect(thrust_input1.output, wheel1.thrust)
connect(thrust_input2.output, wheel2.thrust)
revolute.phi ~ deg2rad(50)*sin(2pi*0.2*t)
connect(wheel2.frame_a, body.frame_b)
end
end
@named model = TestWheel()
model = complete(model)
ssys = structural_simplify(multibody(model))
defs = Dict(unknowns(ssys) .=> 0)
prob = ODEProblem(ssys, defs, (0.0, 10.0))
sol = solve(prob, Rodas5P())
@test SciMLBase.successful_retcode(sol)
render(model, sol, show_axis=true, x=1, y=-1.8, z=5, lookat=[1,-1.8,0], traces=[model.wheel1.frame_a, model.wheel2.frame_a], filename="drifting.gif")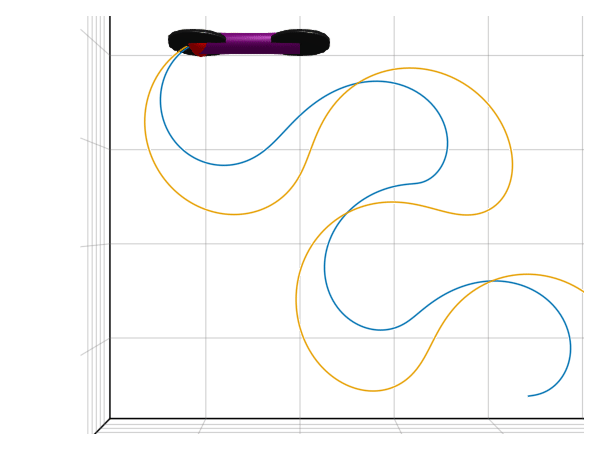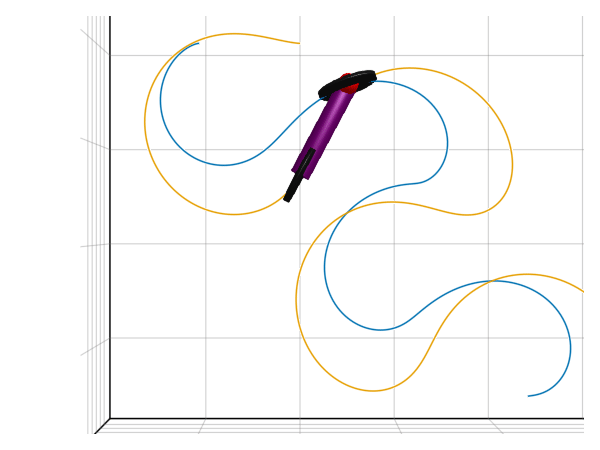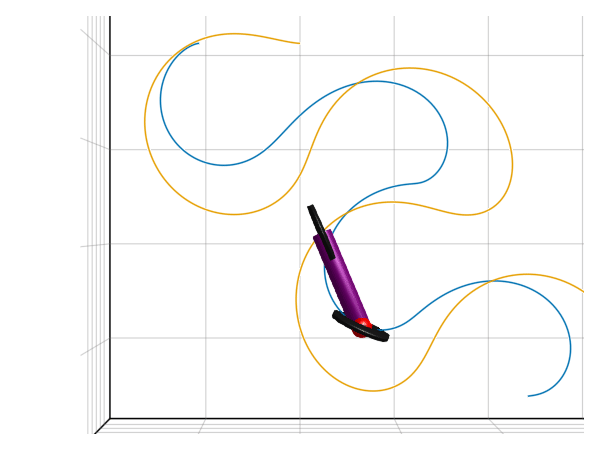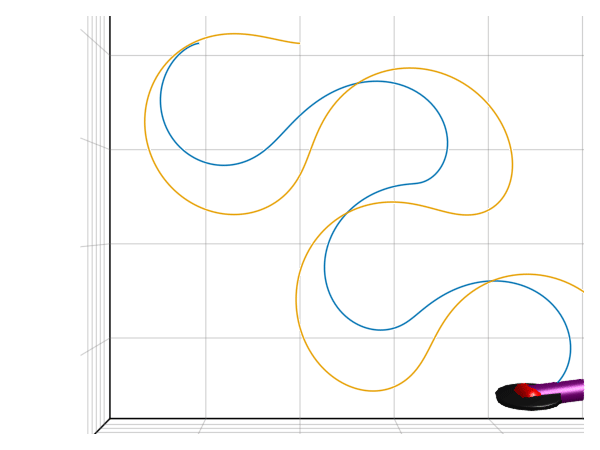
Slip-based planar wheel
This example demonstrates use of the PlanarMechanics.SlipBasedWheelJoint component, which is a more advanced 2D wheel component with slip-dependent friction characteristics. The wheel is being driven by a constant torque, and is connected through a PlanarMechanics.Prismatic joint to a PlanarMechanics.Revolute joint. This forces the wheel to move in a circular arc around the revolute pivot point, and spiral outwards due to slip. A `PlanarMechanics.Body attached to the end of the prismatic joint is used to add inertial properties.
using Multibody
using ModelingToolkit
import ModelingToolkitStandardLibrary.Mechanical.Rotational
import ModelingToolkitStandardLibrary.Blocks
import Multibody.PlanarMechanics as Pl
using Plots
using OrdinaryDiffEq
using LinearAlgebra
using JuliaSimCompiler
using Test
t = Multibody.t
D = Differential(t)
tire_black = [0.1, 0.1, 0.1, 1]
@mtkmodel TestSlipBasedWheel begin
@components begin
slipBasedWheelJoint = Pl.SlipBasedWheelJoint(
radius = 0.3,
r = [1,0], # Driving direction at angle phi = 0
mu_A = 0.8, # Friction coefficient at adhesion
mu_S = 0.4, # Friction coefficient at sliding
N = 100, # Base normal load
sAdhesion = 0.04, # Adhesion slippage
sSlide = 0.12, # Sliding slippage
vAdhesion_min = 0.05, # Minimum adhesion velocity
vSlide_min = 0.15, # Minimum sliding velocity
color = tire_black,
)
prismatic = Pl.Prismatic(r = [0,1], s = 1, v = 0)
revolute = Pl.Revolute(phi = 0, w = 0)
fixed = Pl.Fixed()
engineTorque = Rotational.ConstantTorque(tau_constant = 2)
body = Pl.Body(m = 10, I = 1, gy=0, phi=0, w=0)
inertia = Rotational.Inertia(J = 1, phi = 0, w = 0)
constant = Blocks.Constant(k = 0)
end
@equations begin
connect(fixed.frame_b, revolute.frame_a)
connect(revolute.frame_b, prismatic.frame_a)
connect(prismatic.frame_b, body.frame_a)
connect(prismatic.frame_b, slipBasedWheelJoint.frame_a)
connect(slipBasedWheelJoint.flange_a, inertia.flange_b)
connect(constant.output, slipBasedWheelJoint.dynamicLoad)
connect(engineTorque.flange, inertia.flange_a)
end
end
@named model = TestSlipBasedWheel()
model = complete(model)
ssys = structural_simplify(multibody(model))
defs = ModelingToolkit.defaults(model)
prob = ODEProblem(ssys, [
model.inertia.w => 1e-10, # This is important, at zero velocity, the friction is ill-defined
model.revolute.frame_b.phi => 0,
model.body.w => 0,
D(model.revolute.frame_b.phi) => 0,
D(model.prismatic.r0[2]) => 0,
], (0.0, 15.0))
sol = solve(prob, Rodas5P())
render(model, sol, show_axis=false, x=0, y=0, z=4, traces=[model.slipBasedWheelJoint.frame_a], filename="slipwheel.gif", cache=false)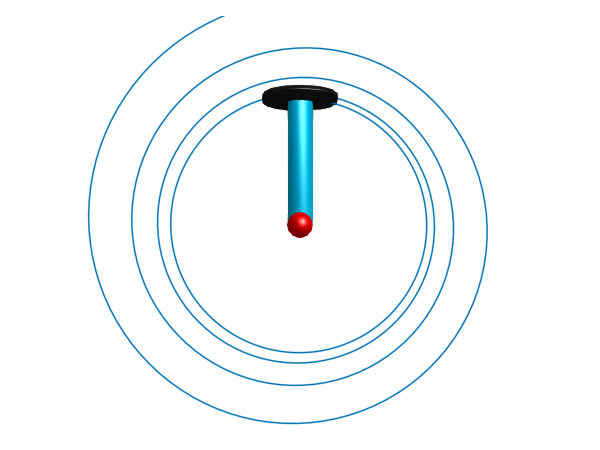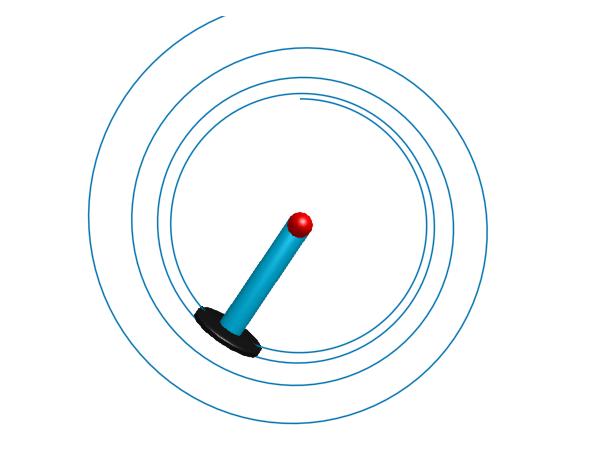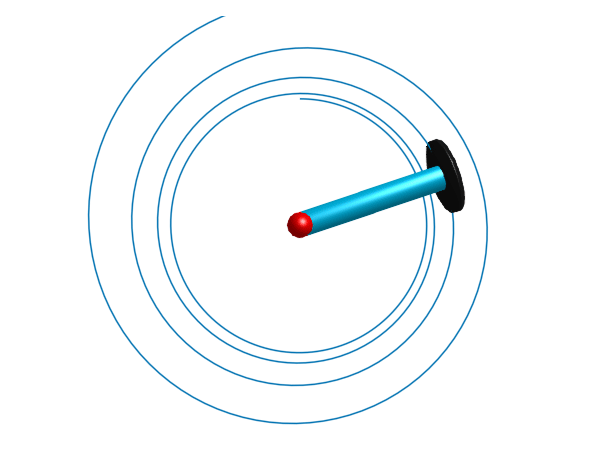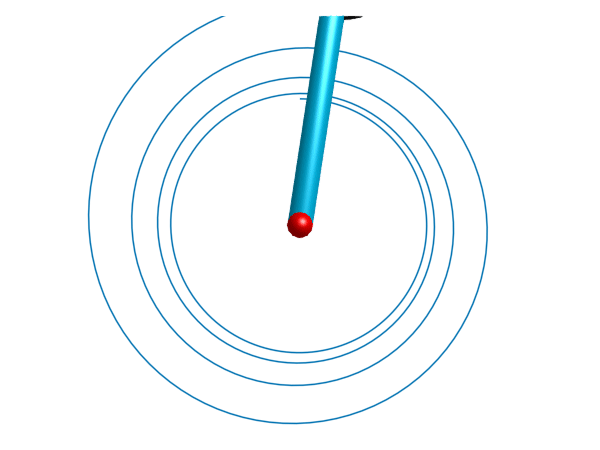
plot(sol, idxs=[
model.slipBasedWheelJoint.w_roll
model.slipBasedWheelJoint.v_long
model.slipBasedWheelJoint.v_slip_long
model.slipBasedWheelJoint.f_long
], layout=4)Planar two-track model
A more elaborate example with 4 wheels.
@mtkmodel TwoTrackWithDifferentialGear begin
@components begin
body = Pl.Body(m = 100, I = 1, gy = 0)
body1 = Pl.Body(m = 300, I = 0.1, r = [1, 1], v = [0, 0], phi = 0, w = 0, gy = 0,)
body2 = Pl.Body(m = 100, I = 1, gy = 0,)
wheelJoint1 = Pl.SlipBasedWheelJoint(
radius = 0.25,
r = [0, 1],
mu_A = 1,
mu_S = 0.7,
N = 1000,
sAdhesion = 0.04,
sSlide = 0.12,
vAdhesion_min = 0.05,
vSlide_min = 0.15,
phi_roll = 0)
wheelJoint2 = Pl.SlipBasedWheelJoint(
radius = 0.25,
r = [0, 1],
mu_A = 1,
mu_S = 0.7,
N = 1500,
sAdhesion = 0.04,
sSlide = 0.12,
vAdhesion_min = 0.05,
vSlide_min = 0.15,
phi_roll = 0)
wheelJoint3 = Pl.SlipBasedWheelJoint(
radius = 0.25,
r = [0, 1],
mu_A = 1,
mu_S = 0.7,
N = 1500,
sAdhesion = 0.04,
sSlide = 0.12,
vAdhesion_min = 0.05,
vSlide_min = 0.15,
phi_roll = 0)
wheelJoint4 = Pl.SlipBasedWheelJoint(
radius = 0.25,
r = [0, 1],
mu_A = 1,
mu_S = 0.7,
N = 1000,
sAdhesion = 0.04,
sSlide = 0.12,
vAdhesion_min = 0.05,
vSlide_min = 0.15,
phi_roll = 0)
differentialGear = Pl.DifferentialGear()
pulse = Blocks.Square(frequency = 1/2, offset = 0, start_time = 1, amplitude = -2)
torque = Rotational.Torque()
constantTorque1 = Rotational.ConstantTorque(tau_constant = 25)
inertia = Rotational.Inertia(J = 1, phi = 0, w = 0)
inertia1 = Rotational.Inertia(J = 1, phi = 0, w = 0)
inertia2 = Rotational.Inertia(J = 1, phi = 0, w = 0)
inertia3 = Rotational.Inertia(J = 1, phi = 0, w = 0)
fixedTranslation1 = Pl.FixedTranslation(r = [0, 2])
fixedTranslation2 = Pl.FixedTranslation(r = [0.75, 0])
fixedTranslation3 = Pl.FixedTranslation(r = [-0.75, 0])
fixedTranslation4 = Pl.FixedTranslation(r = [0.75, 0])
fixedTranslation5 = Pl.FixedTranslation(r = [-0.75, 0])
leftTrail = Pl.FixedTranslation(r = [0, -0.05])
rightTrail = Pl.FixedTranslation(r = [0, -0.05])
revolute = Pl.Revolute(axisflange=true)
revolute2 = Pl.Revolute(axisflange=true, phi = -0.43633231299858, w = 0)
dynamic_load = Blocks.Constant(k=0)
end
@equations begin
connect(wheelJoint2.flange_a, inertia1.flange_b)
connect(inertia.flange_b, wheelJoint1.flange_a)
connect(fixedTranslation2.frame_b, fixedTranslation1.frame_a)
connect(fixedTranslation2.frame_a, wheelJoint2.frame_a)
connect(fixedTranslation3.frame_b, fixedTranslation1.frame_a)
connect(wheelJoint3.frame_a, fixedTranslation3.frame_a)
connect(inertia2.flange_b, wheelJoint3.flange_a)
connect(body1.frame_a, fixedTranslation1.frame_a)
connect(fixedTranslation1.frame_b, fixedTranslation4.frame_b)
connect(fixedTranslation1.frame_b, fixedTranslation5.frame_b)
connect(inertia3.flange_b, wheelJoint4.flange_a)
connect(pulse.output, torque.tau)
connect(differentialGear.flange_right, wheelJoint3.flange_a)
connect(differentialGear.flange_left, wheelJoint2.flange_a)
connect(constantTorque1.flange, differentialGear.flange_b)
connect(body.frame_a, leftTrail.frame_b)
connect(leftTrail.frame_b, wheelJoint1.frame_a)
connect(body2.frame_a, rightTrail.frame_b)
connect(wheelJoint4.frame_a, rightTrail.frame_b)
connect(leftTrail.frame_a, revolute2.frame_a)
connect(revolute2.frame_b, fixedTranslation4.frame_a)
connect(torque.flange, revolute.flange_a, revolute2.flange_a)
connect(revolute.frame_a, rightTrail.frame_a)
connect(revolute.frame_b, fixedTranslation5.frame_a)
connect(dynamic_load.output, wheelJoint1.dynamicLoad, wheelJoint2.dynamicLoad, wheelJoint3.dynamicLoad, wheelJoint4.dynamicLoad)
end
end
@named model = TwoTrackWithDifferentialGear()
model = complete(model)
ssys = structural_simplify(multibody(model))
defs = merge(
Dict(unknowns(ssys) .=> 0),
ModelingToolkit.defaults(model),
Dict(model.body.w => 0),
)
prob = ODEProblem(ssys, defs, (0.0, 5.0))
sol = solve(prob, Rodas5P(autodiff=false))
@test SciMLBase.successful_retcode(sol)
Multibody.render(model, sol, show_axis=false, x=0, y=0, z=5, filename="twotrack.gif", cache=false) ```
```