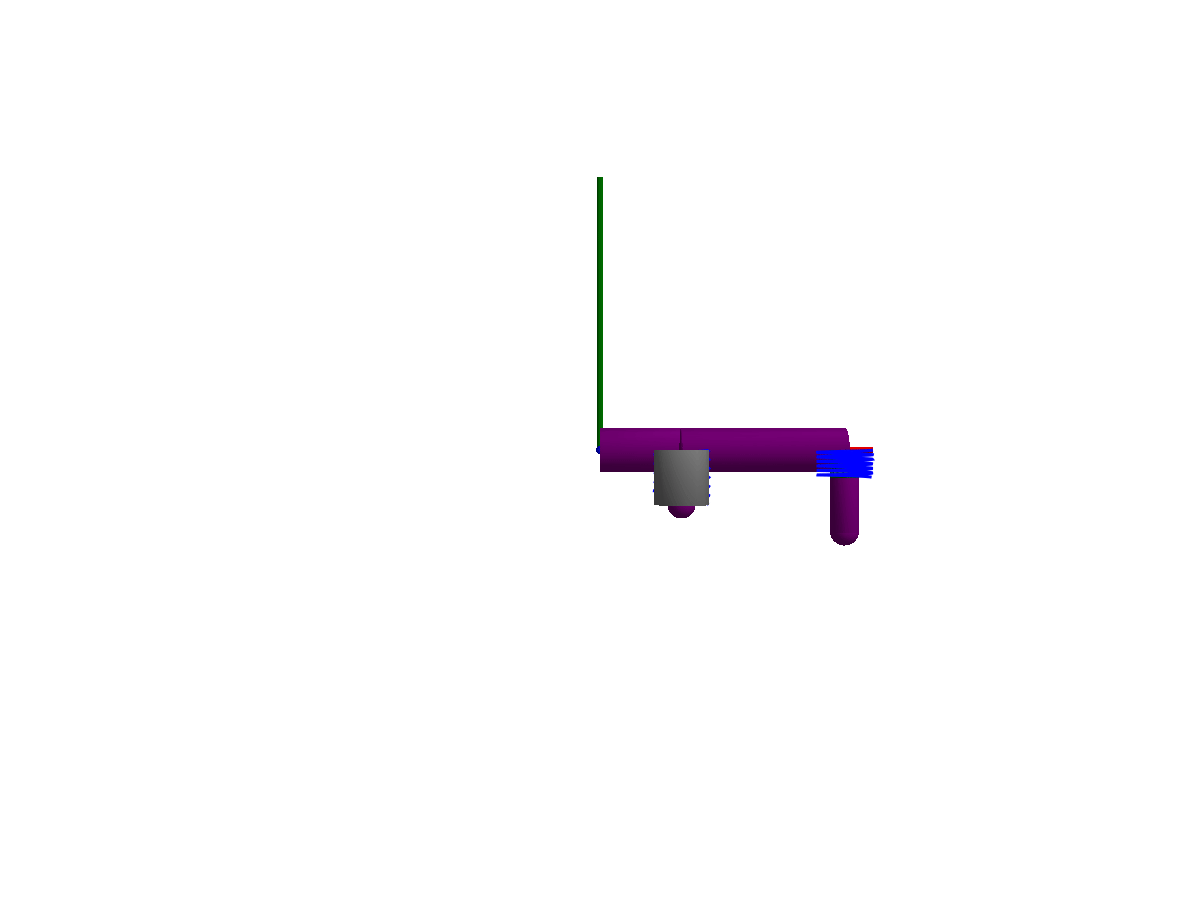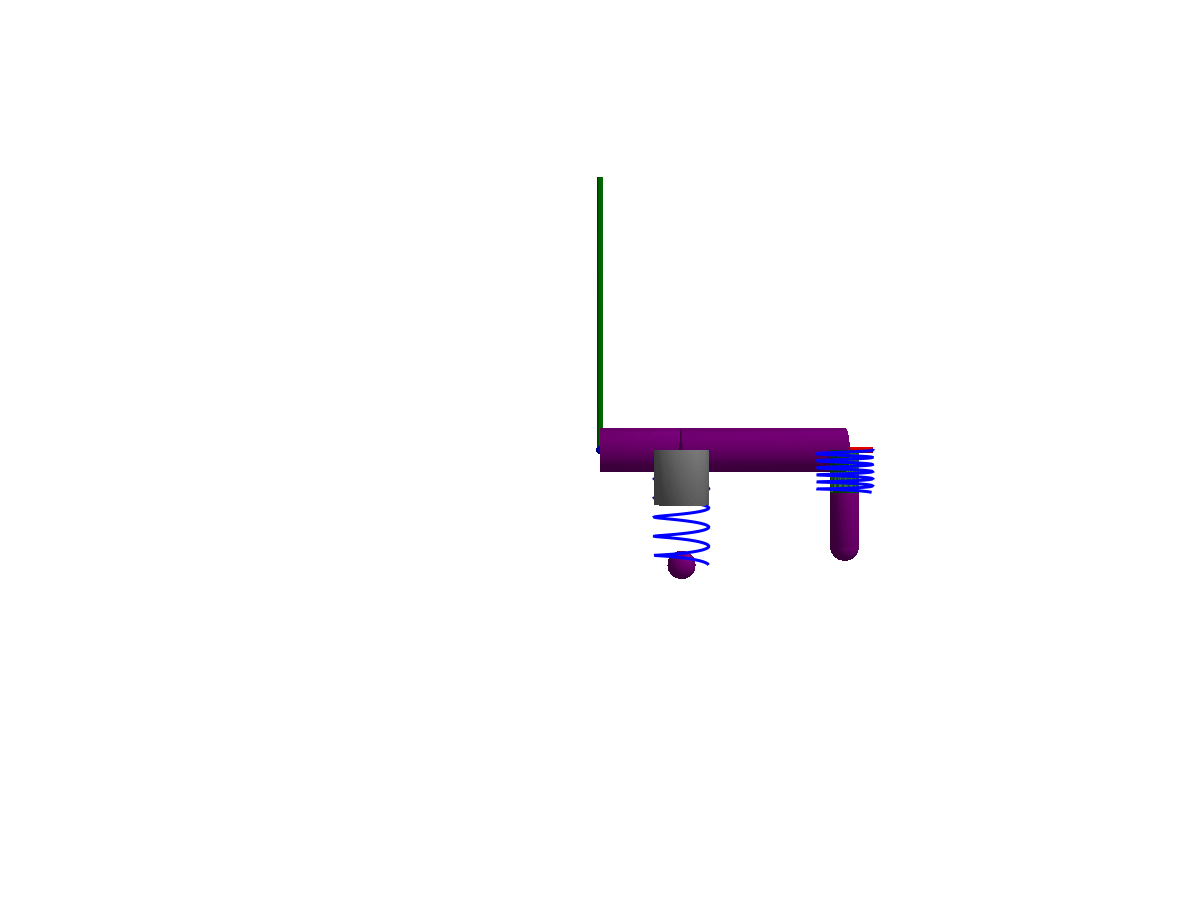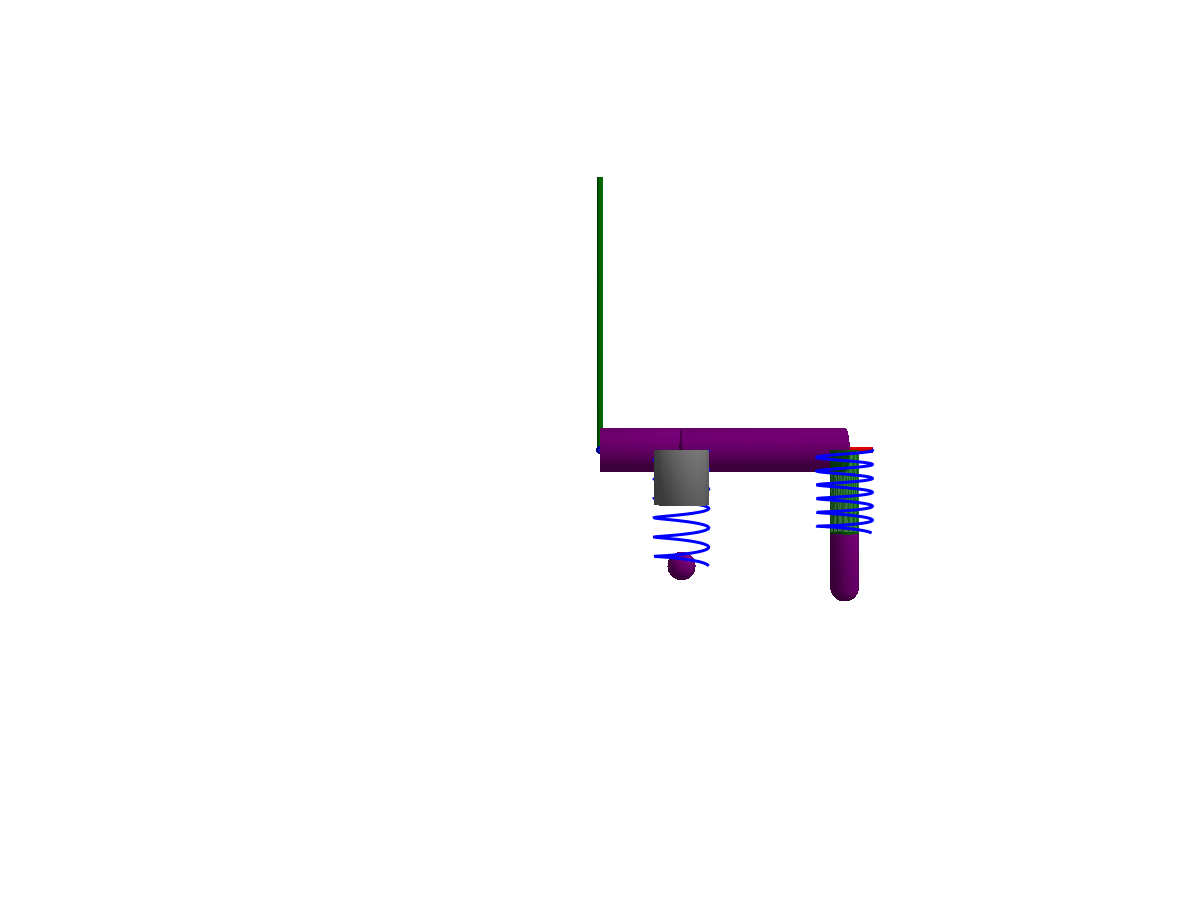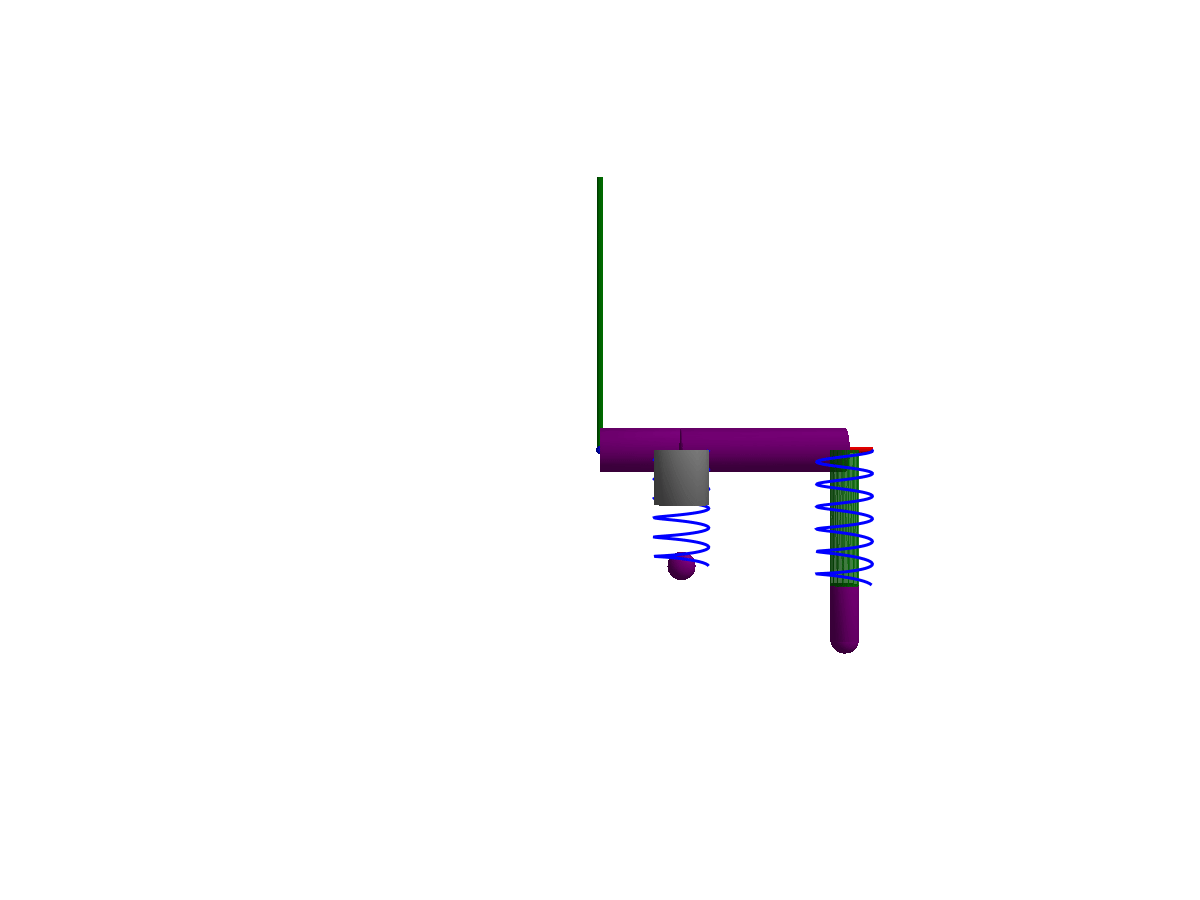Multibody

Documentation for Multibody.

Welcome to the world of Multibody.jl, a powerful and flexible component of JuliaSim designed to model, analyze, and simulate multibody systems in Julia. As a state-of-the-art tool, Multibody.jl enables users to efficiently study the dynamics of complex mechanical systems in various fields, such as robotics, biomechanics, aerospace, and vehicle dynamics.

Built on top of the Julia language and the JuliaSim suite of tools for modeling, simulation, optimization and control, Multibody.jl harnesses the power of Julia's high-performance computing capabilities, making it a go-to choice for both researchers and engineers who require fast simulations and real-time performance. With an intuitive syntax and a comprehensive set of features, this package seamlessly integrates with other Julia and JuliaSim libraries, enabling users to tackle diverse and sophisticated problems in multibody dynamics.

In this documentation, you will find everything you need to get started with Multibody.jl, from basic component descriptions to detailed examples showcasing the package's capabilities. As you explore this documentation, you'll learn how to create complex models, work with forces and torques, simulate various types of motions, and visualize your results in both 2D and 3D. Whether you are a seasoned researcher or a newcomer to the field, Multibody.jl will empower you to bring your ideas to life and unlock new possibilities in the fascinating world of multibody dynamics.

Example overview

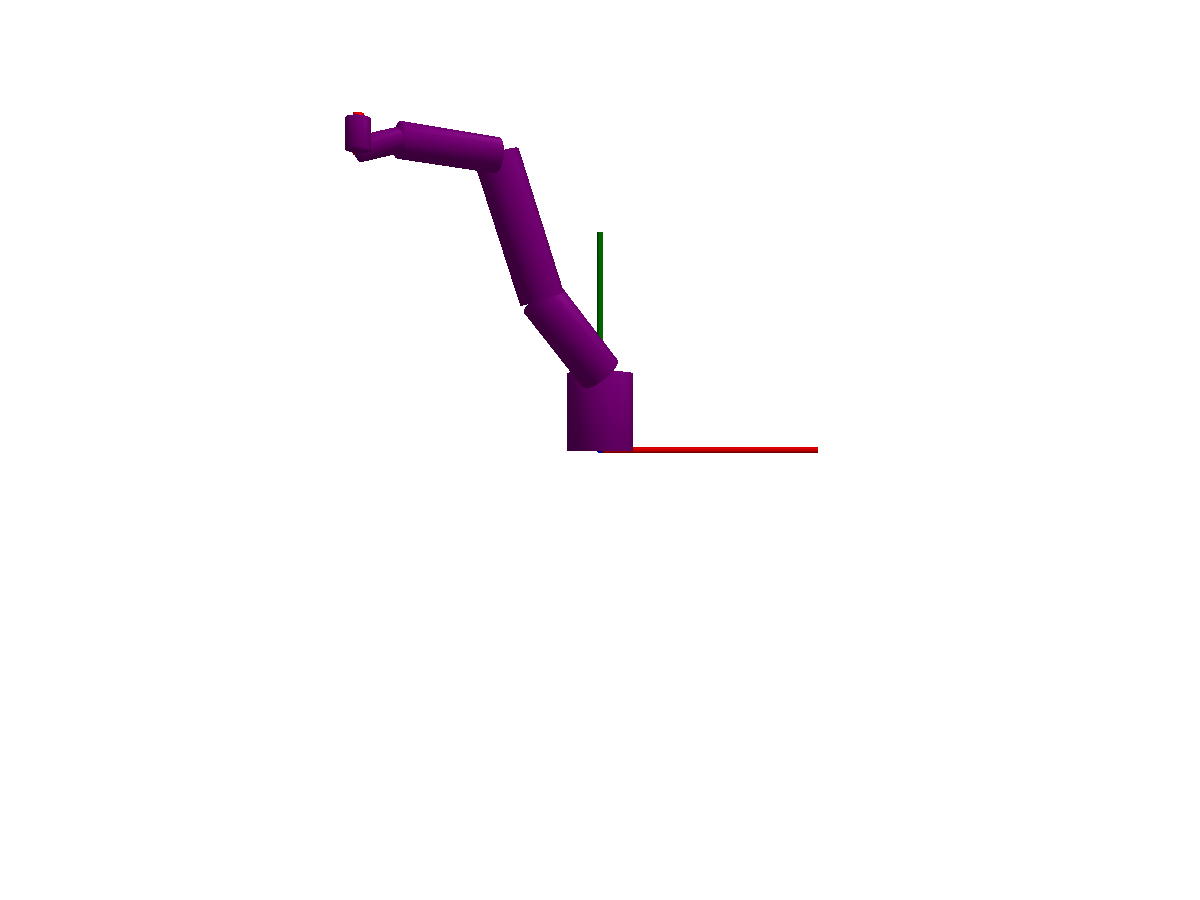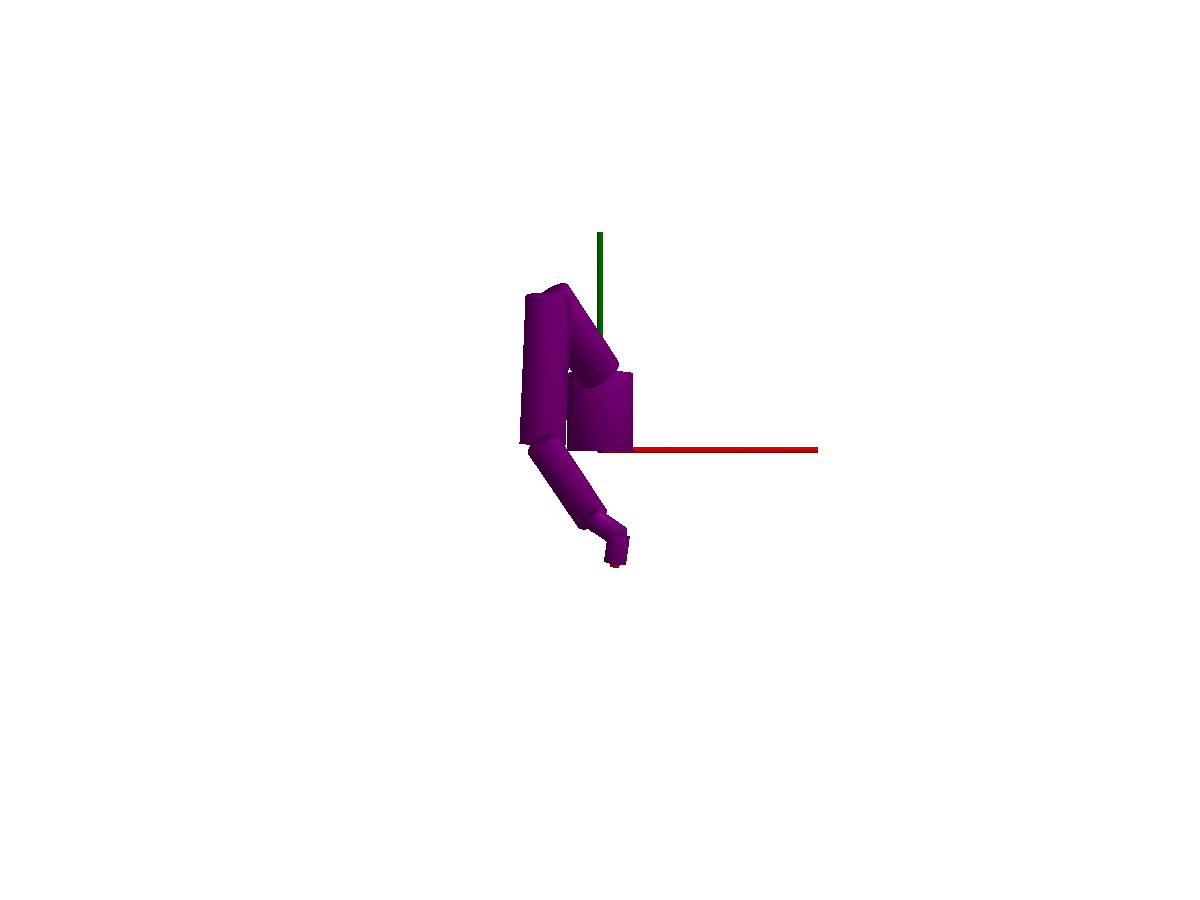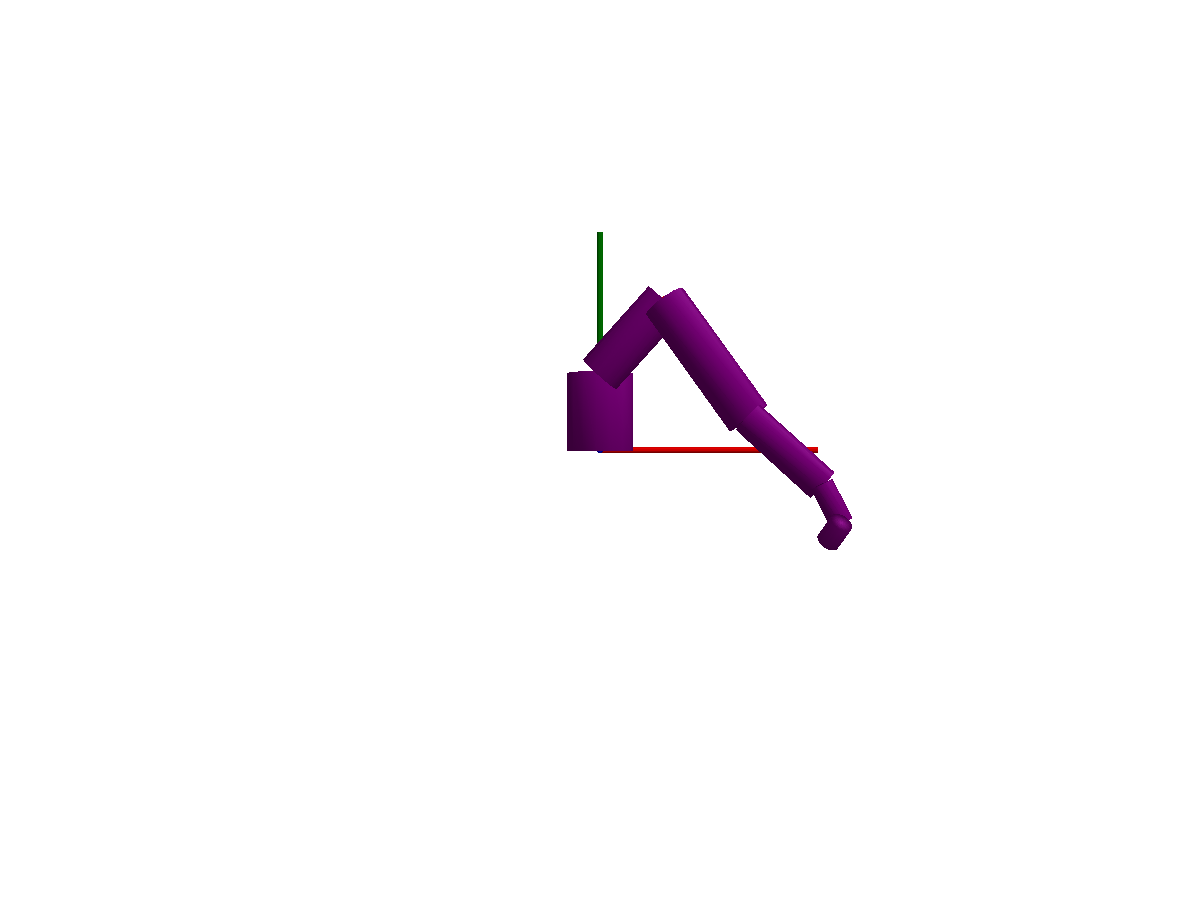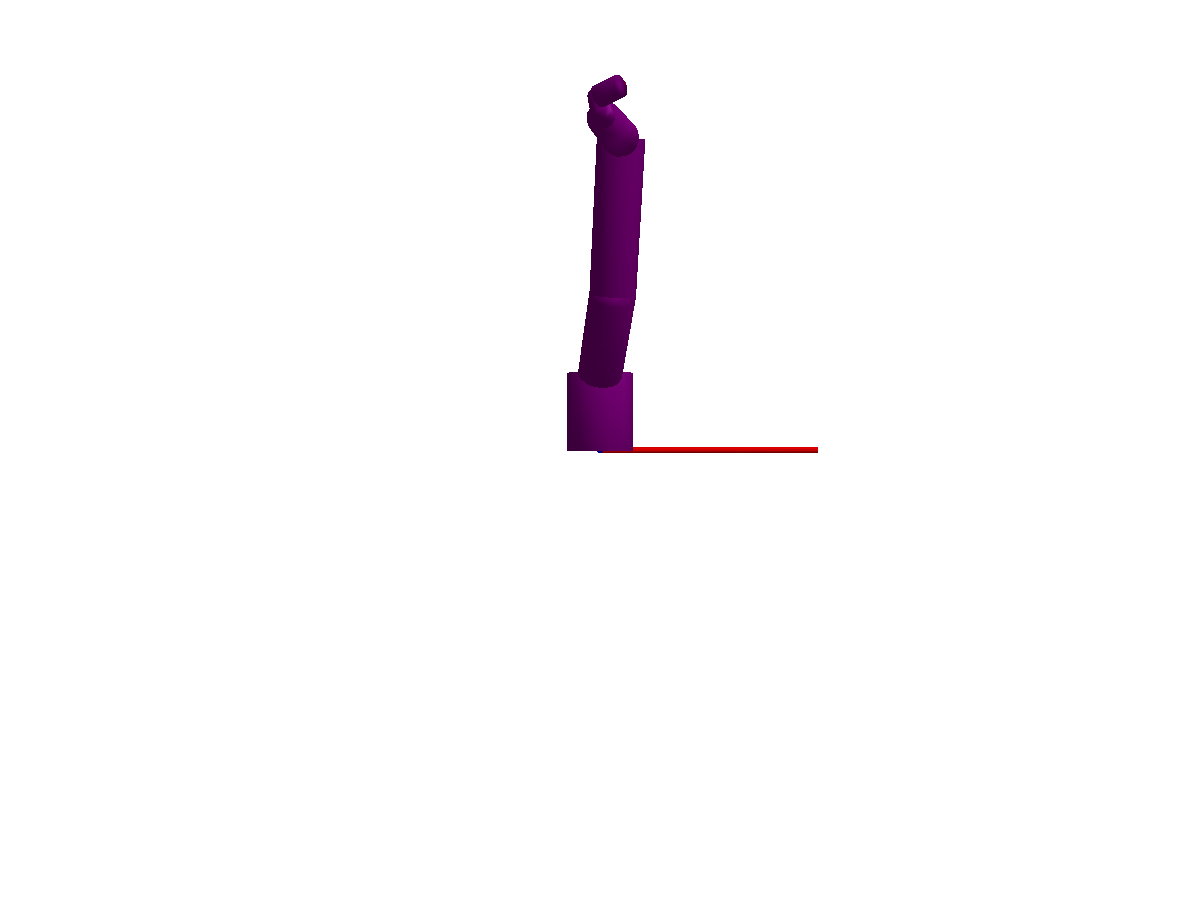
The following animations give a quick overview of simple mechanisms that can be modeled using Multibody.jl. The examples are ordered from simple at the top, to more advanced at the bottom. Please browse the examples for even more examples!

Installation

To install this library, first follow the installation instructions for JuliaSimCompiler. In particular, you need to add the JuliaHub Registry.

After the registry is added and JuliaSimCompiler is installed, you may install this package using

import Pkg
Pkg.add("Multibody")

Notable differences from Modelica

• The torque variable in Multibody.jl is typically called tau rather than t to not conflict with the often used independent variable t used to denote time.
• Multibody.jl occasionally requires the user to specify which component should act as the root of the kinematic tree. This only occurs when bodies are connected directly to force components without a joint parallel to the force component.
• In Multibody.jl, the orientation object of a Frame is accessed using the function ori.
• Quaternions in Multibody.jl follow the order $[s, i, j, k]$, i.e., scalar/real part first.

2D and 3D modeling

Multibody.jl offers components for modeling in both 2D and 3D. 2D modeling, often referred to as planar mechanics, is a subset of 3D modeling where the motion is constrained to a plane, the x,y plane. Planar mechanics is sometimes referred to as 3 degrees of freedom (DOF) modeling, referring to the 2 translational DOF and one rotational DOF that the plane offers. Most components in Multibody.jl are aimed at 3D modeling (sometimes referred to as 6 DOF modeling), but components for 2D modeling exist in the submodule Multibody.PlanarMechanics.

The components from ModelingToolkitStandardLibrary.Mechanical are 1D, i.e., a single degree of freedom only. These components can be used in both 2D and 3D modeling together with Multibody components that have support for attaching 1D components, such as joints supporting the axisflange keyword.