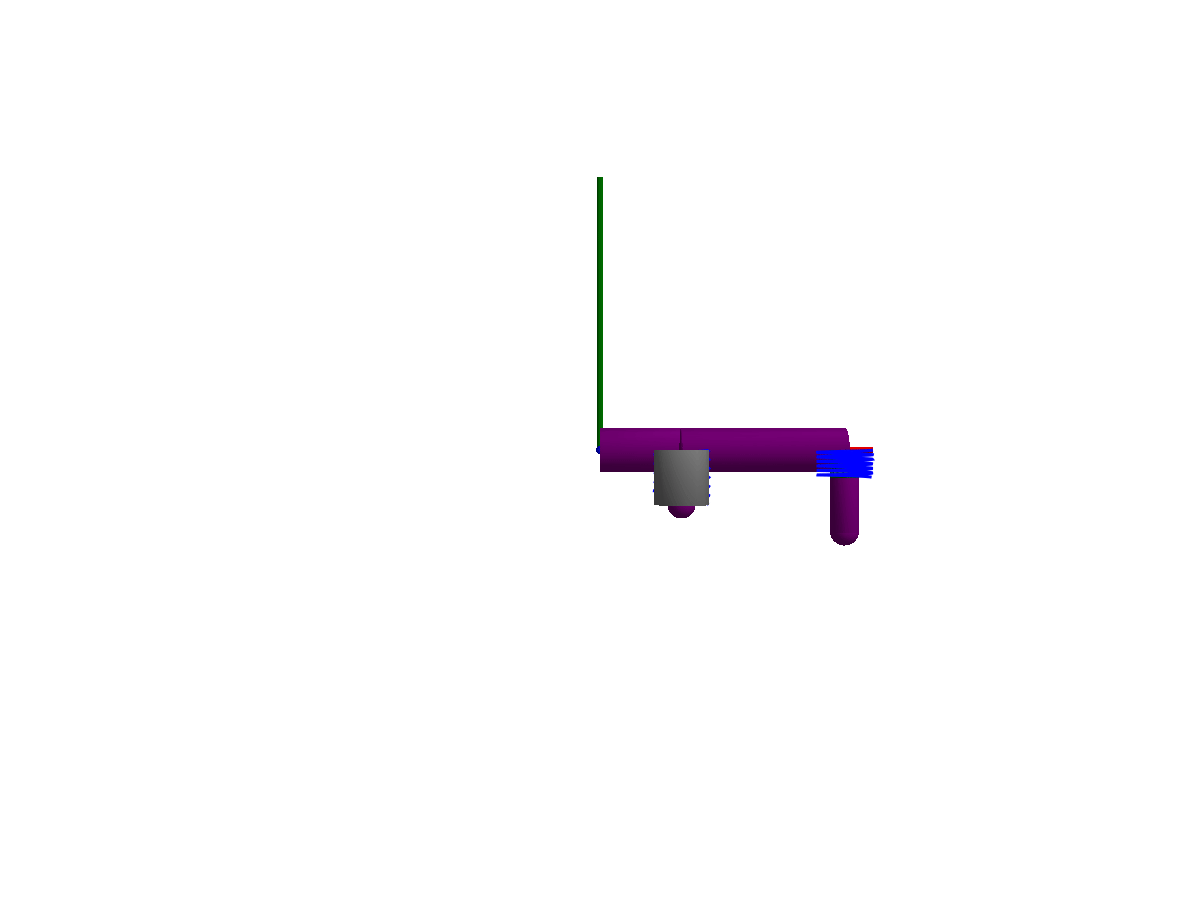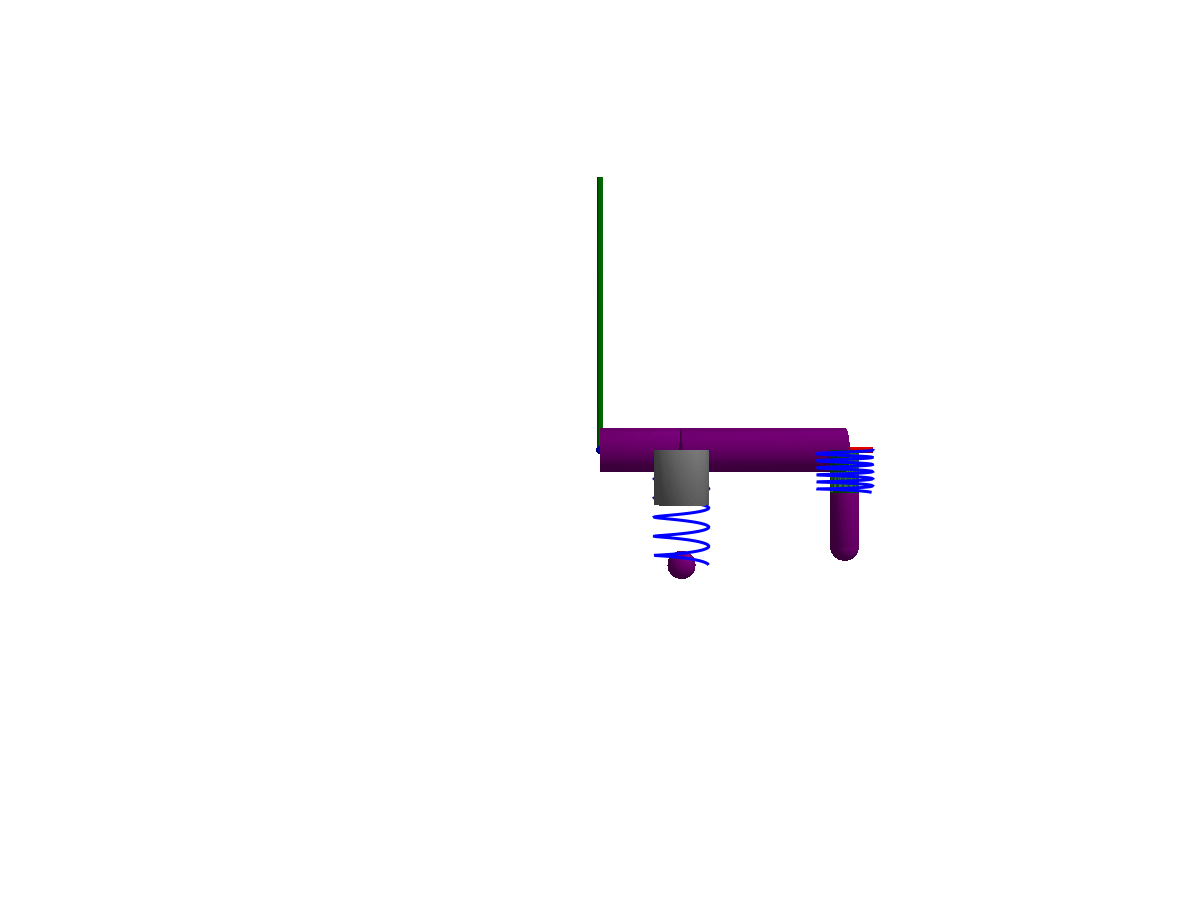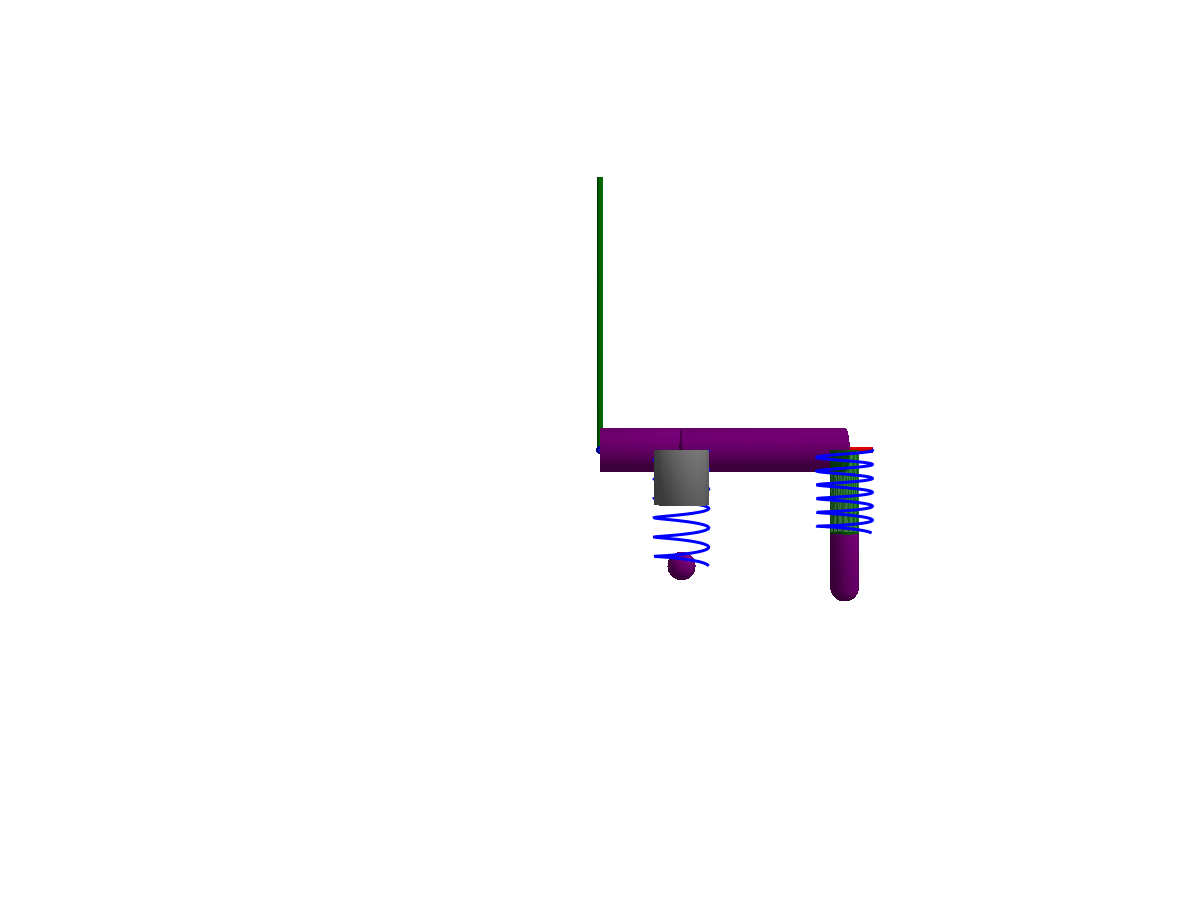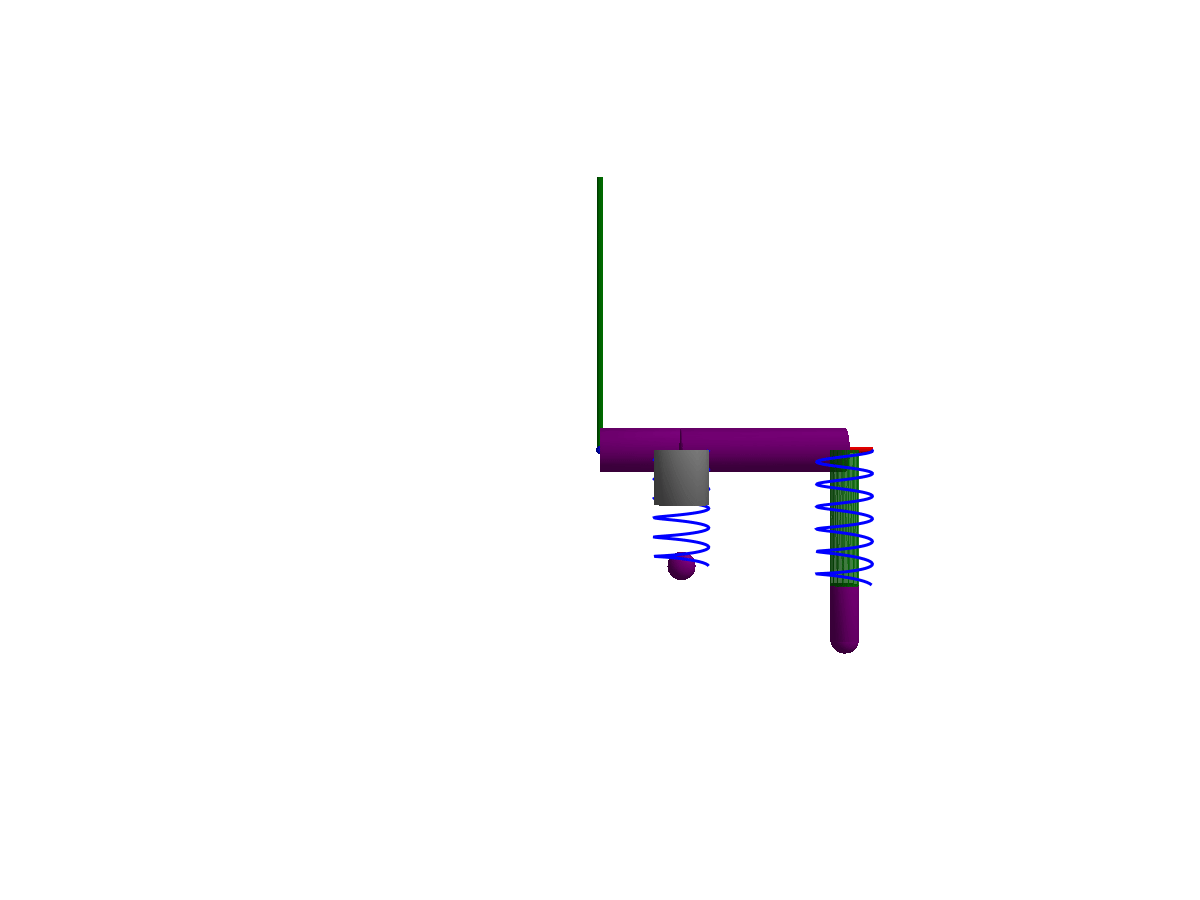Spring-damper system

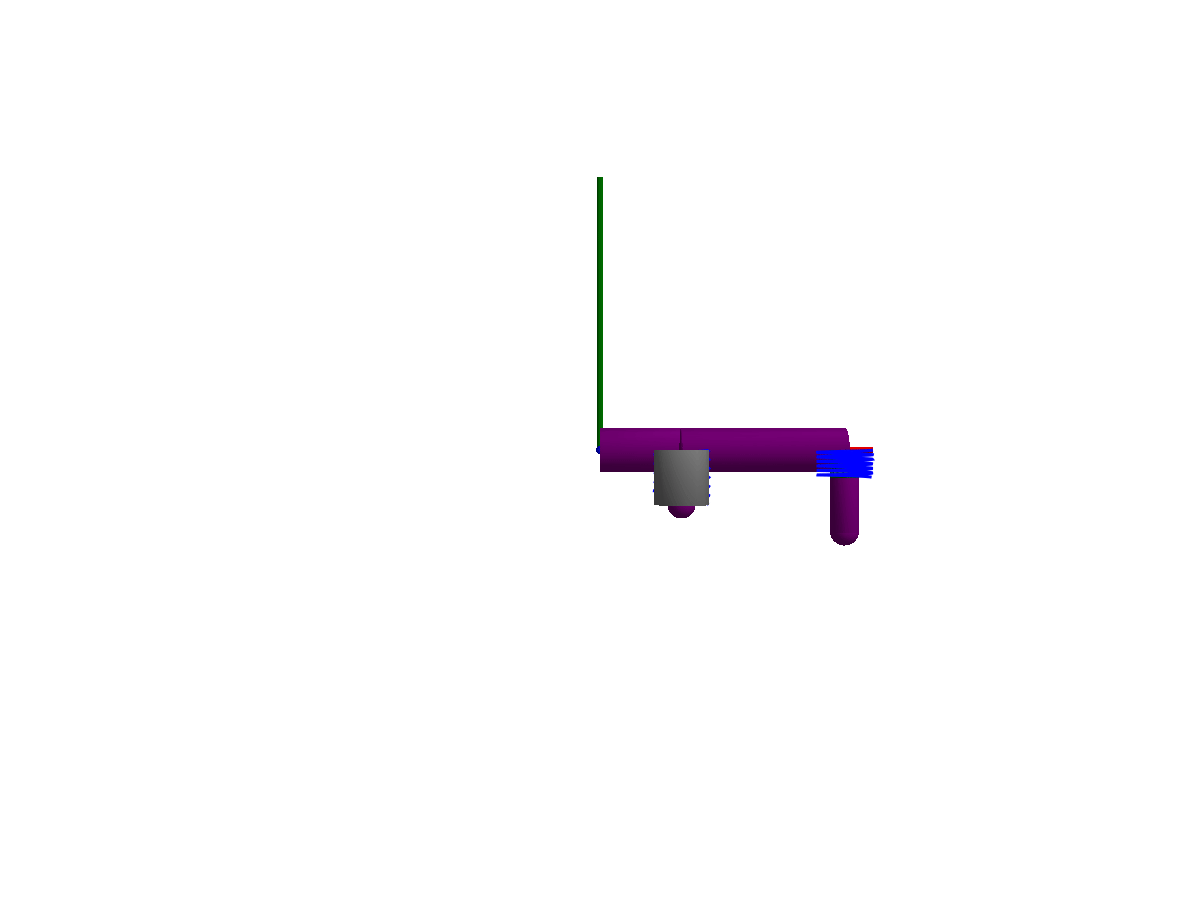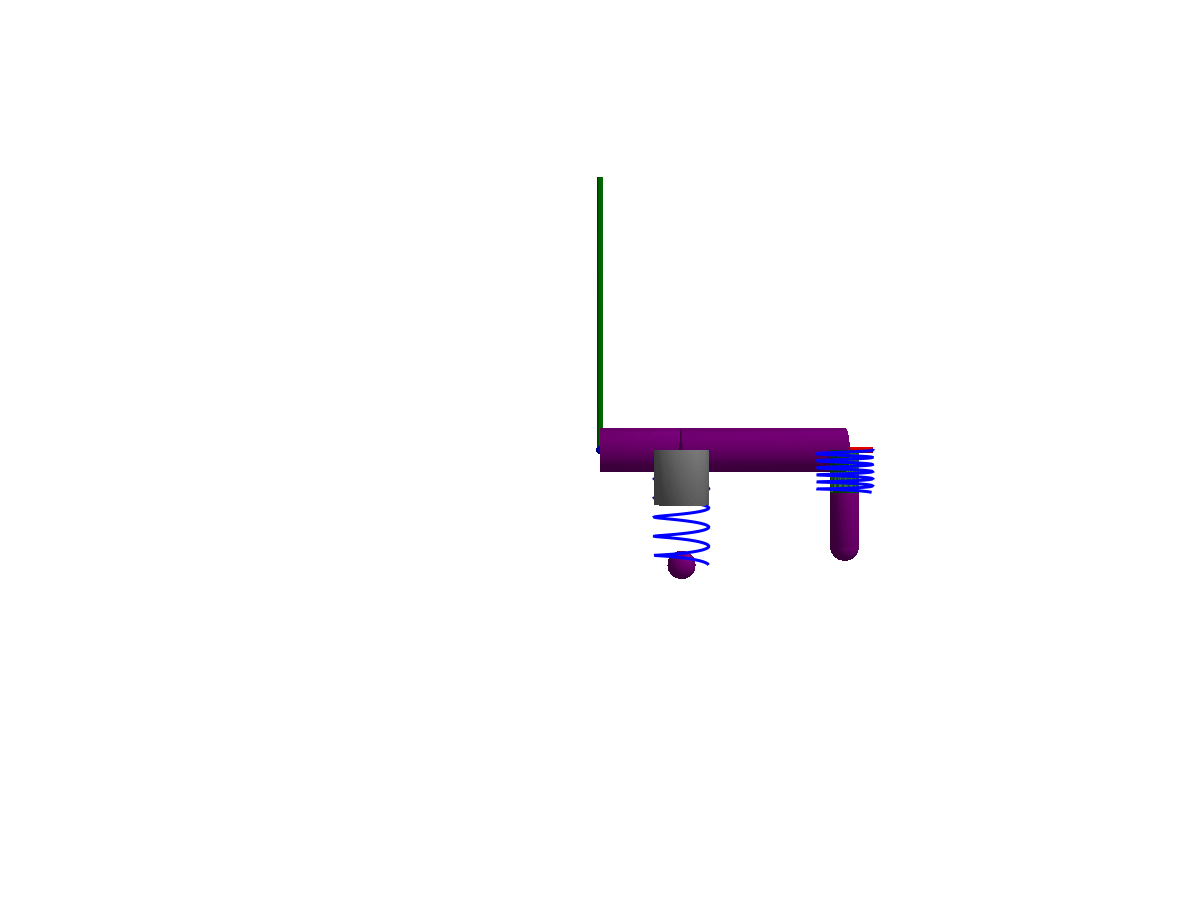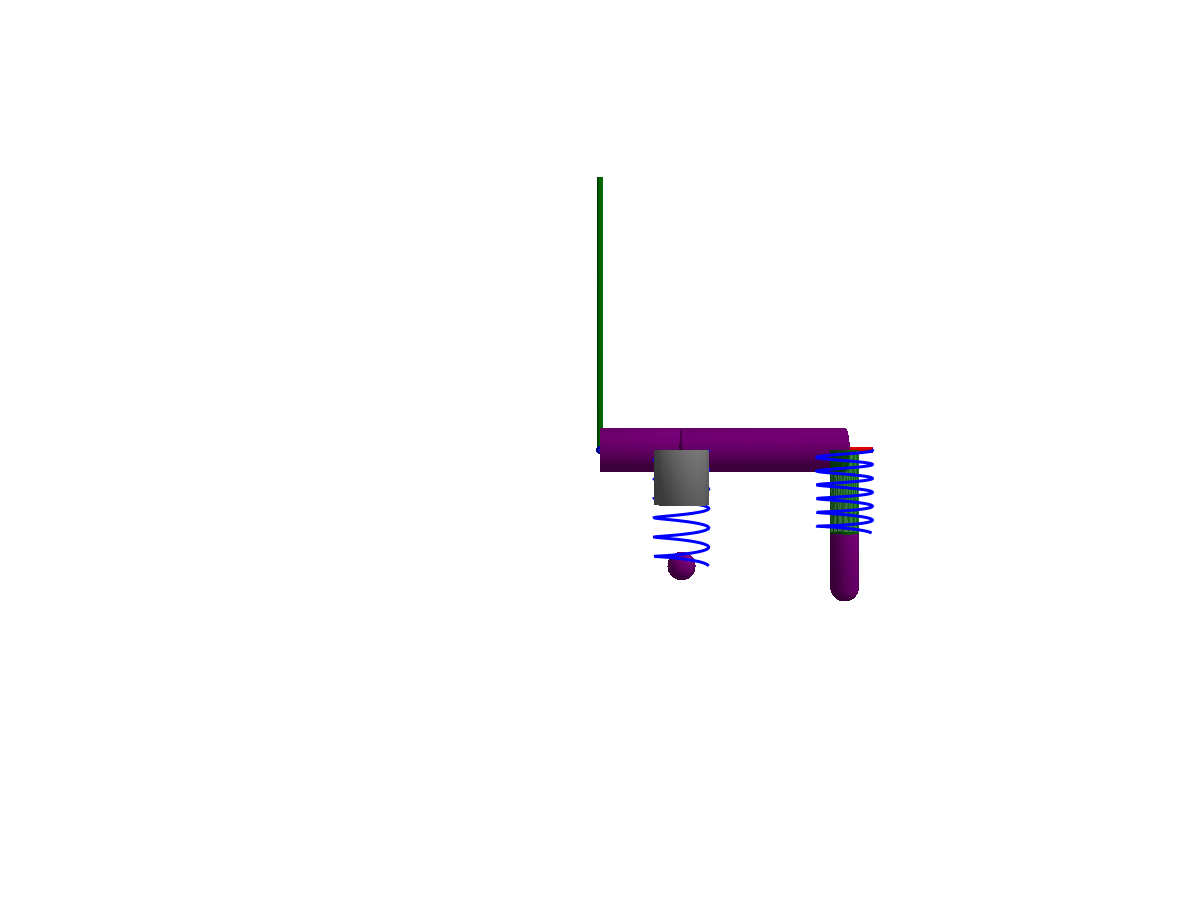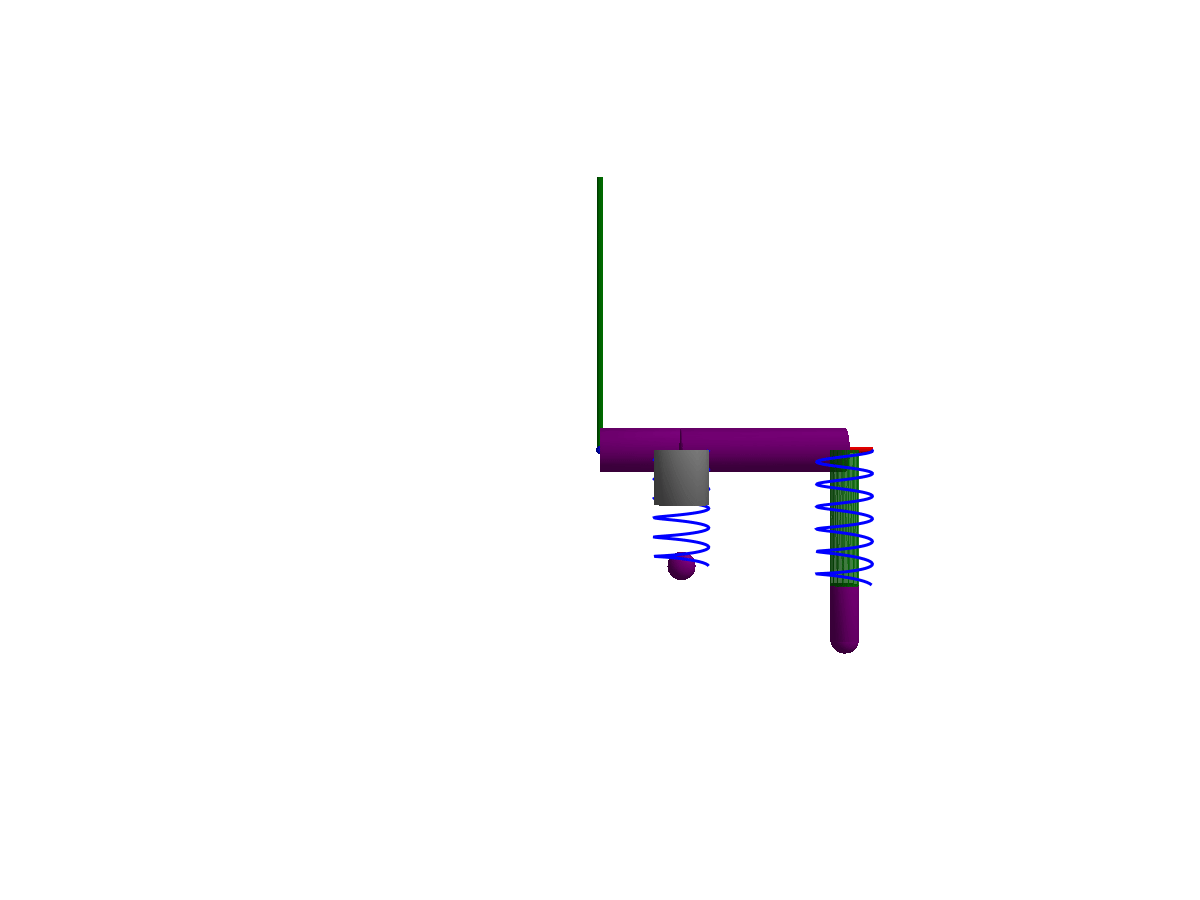
Welcome to the spring-damper system example, where we will show you the process of modeling and simulating a basic yet essential mechanical system using the powerful Multibody.jl package in JuliaSim. By understanding the underlying principles of spring-damper systems, you will gain valuable insights into the behavior of various real-world systems, such as suspension systems in vehicles, vibration isolation mechanisms, and biomechanical structures.

This tutorial mirrors that of the following Modelica tutorial Spring damper system and demonstrates that a body can be freely moving without any connection to a joint. In this case body coordinates are used as state by setting the option isroot=true to the body.

This example has two parallel spring-mass parts, the first body (body1) is attached directly to the spring, with no joint in parallel with the spring. In this situation, we have to set isroot=true for body1 to indicate that we want to use the body variables as state. The second body (body2) is attached to the spring with a joint in parallel with the spring, so we can use the joint variables as state, hence isroot=false for body2.

using Multibody
using ModelingToolkit
using Plots
using JuliaSimCompiler
using OrdinaryDiffEq

t = Multibody.t
D = Differential(t)
world = Multibody.world
@named begin
    body1 = Body(; m = 1, isroot = true, r_cm = [0.0, 0, 0], I_11 = 0.1, I_22 = 0.1,
                 I_33 = 0.1, r_0 = [0.3, -0.2, 0]) # This is root since there is no joint parallel to the spring leading to this body
    body2 = Body(; m = 1, isroot = false, r_cm = [0.0, -0.2, 0]) # This is not root since there is a joint parallel to the spring leading to this body
    bar1 = FixedTranslation(r = [0.3, 0, 0])
    bar2 = FixedTranslation(r = [0.6, 0, 0])
    p2 = Prismatic(n = [0, -1, 0], s0 = 0.1, axisflange = true)
    spring2 = Multibody.Spring(c = 30, s_unstretched = 0.1)
    spring1 = Multibody.Spring(c = 30, s_unstretched = 0.1)
    damper1 = Multibody.Damper(d = 2)
end
eqs = [connect(world.frame_b, bar1.frame_a)
       connect(bar1.frame_b, bar2.frame_a)
       connect(bar2.frame_b, p2.frame_a)
       connect(p2.frame_b, body2.frame_a)
       connect(bar2.frame_b, spring2.frame_a)
       connect(body2.frame_a, spring2.frame_b)
       connect(damper1.frame_a, bar1.frame_b)
       connect(spring1.frame_a, bar1.frame_b)
       connect(damper1.frame_b, body1.frame_a)
       connect(spring1.frame_b, body1.frame_a)]

@named model = ODESystem(eqs, t,
                         systems = [
                             world,
                             body1,
                             body2,
                             bar1,
                             bar2,
                             p2,
                             spring1,
                             spring2,
                             damper1,
                         ])

ssys = structural_simplify(multibody(model))

prob = ODEProblem(ssys, [
    damper1.d => 2;
    collect(body1.v_0) .=> 0;
    collect(body1.w_a) .=> 0;
], (0, 5))

sol = solve(prob, Rodas4())
@assert SciMLBase.successful_retcode(sol)

Plots.plot(
    Plots.plot(sol, idxs = [spring1.s, spring2.s]),
    Plots.plot(sol, idxs = [body1.r_0[2], body2.r_0[2]]),
    Plots.plot(sol, idxs = [spring1.f, spring2.f]),
)

In this example we used separate springs and dampers, see also the component SpringDamperParallel which combines the two in one component.

3D animation

Multibody.jl supports automatic 3D rendering of mechanisms, we use this feature to illustrate the result of the simulation below:

import GLMakie
Multibody.render(model, sol; filename = "springdamper.gif")