Parametric uncertainty quantification

In JuliaSimModelOptimizer one can perform parametric uncertainty quantification using parametric_uq with an InverseProblem. The result of a parametric_uq call is a set of parameters which sufficiently fit all experiments to their respective data simultaneously. We refer to this as the ensemble of plausible parameters.

The parametric_uq Function

JuliaSimModelOptimizer.parametric_uq — Function
parametric_uq(prob, alg; sample_size, adtype = Optimization.AutoForwardDiff(), progress = true)

Create an ensemble of the given size of possible solutions for the inverse problem using the method specified by alg. This can be seen as a representation of the parametric uncertainty characterizing the given inverse problem. This is also called a multimodel in some domains.

Arguments

Keyword Arguments

  • sample_size: Required. Number of samples to generate.
  • adtype: Automatic differentiation choice, see the Optimization.jl docs for details. Defaults to AutoForwardDiff().
  • progress: Show the progress of the optimization (current loss value) in a progress bar. Defaults to true.

Stochastic Optimization

If alg is a StochGlobalOpt method, the optimization algorithm runs until convergence or until maxiters has been reached. This process is repeated a number of times equal to sample_size to create an ensemble of possible parametrizations.

source

Optimization Methods

The following are the choices of algorithms which are available for controlling the parametric uncertainty quantification process:

JuliaSimModelOptimizer.StochGlobalOpt — Type
StochGlobalOpt(; method = SingleShooting(optimizer = BBO_adaptive_de_rand_1_bin_radiuslimited(), maxiters = 10_000), parallel_type = EnsembleSerial())

A stochastic global optimization method.

Keyword Arguments

  • parallel_type: Choice of parallelism. Defaults to EnsembleSerial() or serial computation. For more information on ensemble parallelism types, see the ensemble types from SciML
  • method: a calibration algorithm to use during the runs. Defaults to SingleShooting(optimizer = BBO_adaptive_de_rand_1_bin_radiuslimited(), maxiters = 10_000). i.e. single shooting method with a black-box differential evolution method from BlackBoxOptimization. For more information on choosing optimizers, see Optimization.jl.
source

Result Types

JuliaSimModelOptimizer.ParameterEnsemble — Type
ParameterEnsemble

The structure contains the result of a parameter ensemble when a StochGlobalOpt method was used to generate the population. To export results to a DataFrame use DataFrame(ps) and to plot them use plot(ps, experiment), where ps is the ParameterEnsemble and experiment is the AbstractExperiment, whose default parameter (or initial condition) values will be used.

source

Importing Parameter ensembles

If an ensemble of parameters was generated in some alternative way, JuliaSimModelOptimizer still allows for importing these values into a ParameterEnsemble to enable using the parametric uncertainty quantification analysis workflow. This is done via the following function:

Analyzing Parameter Ensemble Results

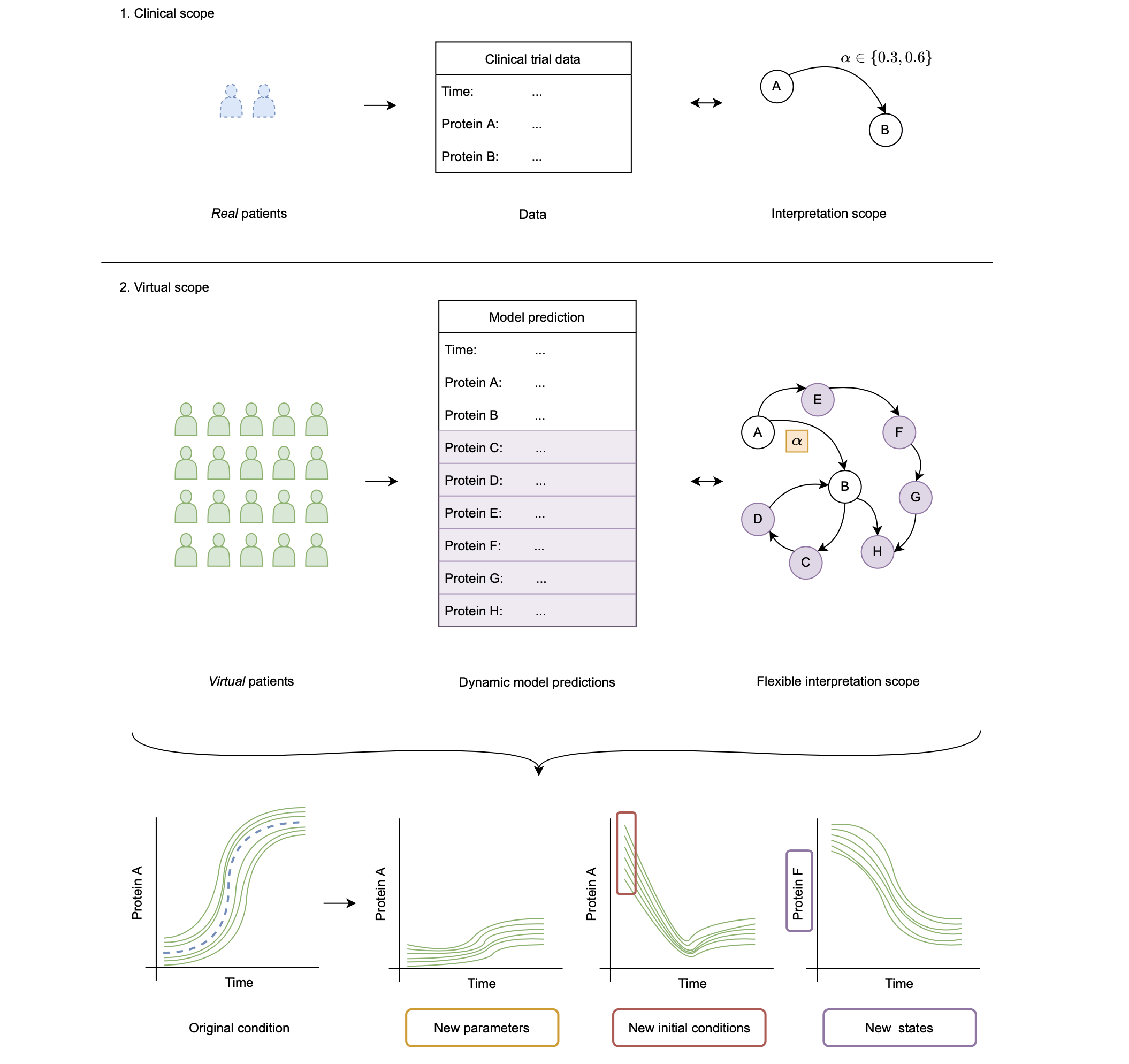
Once parameters (PS) are generated given some multi-experiment data, we can use them to expand our analysis scope to dimensions where, for example, experimental data collection is difficult. This objective is schematically shown in the figure below. Here, we summarise three groups:

  1. We can use the PS to model the system for new values of model parameters. Note that here we refer to model parameters not as parameters that specify a patient, but other, independent parameters of the model. As an example we have the reaction rate α.
  2. We can use the PS to model the system for new initial conditions for the observed states of the system. Here, this relates to Protein A and B.
  3. We can use the PS to model states of the system that have not been observed. These are Protein C to H in this example.

Objective of PSs

The following functions enable such analyses: