Getting started with linear control
This page will guide the user through how build and manipulate linear models, and to perform linear control design for a simple system in multiple different ways.
More detailed tutorials on each topic are available in the tutorials section.
Linear models
Linear models are built and manipulated using the tools from ControlSystems.jl and RobustAndOptimalControl.jl. See the documentation on creating and manipulating systems to get started.
Time and frequency domain analysis of linear systems
See Time and frequency response analysis to get started.
Analysis of linear systems
To get started with classical robustness analysis of linear systems, see Analysis of linear control systems as well as the video below.
Design examples: The system model
The following sections include introductory examples to get you started with linear control design. Throughout, we will consider a simple model of two masses connected by a spring and a viscous damper, depicted below. 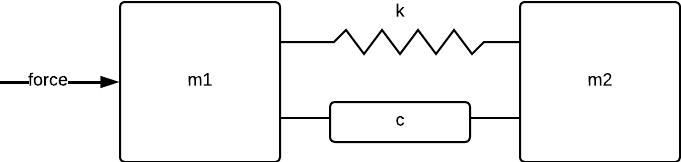
This model is predefined in the module DemoSystems:
using DyadControlSystems, Plots
P = DemoSystems.double_mass_model() # The function `double_mass_model` returns a `StateSpace` objectStateSpace{Continuous, Float64}
A =
0.0 1.0 0.0 0.0
-100.0 -2.0 100.0 1.0
0.0 0.0 0.0 1.0
100.0 1.0 -100.0 -2.0
B =
0.0
1.0
0.0
0.0
C =
1.0 0.0 0.0 0.0
D =
0.0
Continuous-time state-space modelWe can plot its Bode plot using bodeplot
bodeplot(P) # See https://juliaplots.org/ for more information on plottingPID control
PID: Manual tuning
A PID controller can be created using the function pid
using DyadControlSystems, Plots
P = DemoSystems.double_mass_model()
C = pid(5, 1, 1, Tf=0.01) # The keyword argument `Tf` specifies the time constant for a lowpass filter.
Gcl = feedback(P*C) # We can form the closed-loop system from reference to output using [`feedback`](@ref)
f1 = bodeplot([P*C, Gcl], lab=["PC" "" "PC/(1+PC)" ""]) # We plot the Bode curve of the loop-transfer function and the closed-loop transfer function
f2 = plot(step(Gcl, 0:0.01:10)) # And plot a step response
plot(f1,f2) # Combine to plots in a single figureFunctions used:
See also the video below, where a simple PID controller is designed for the double-mass model, and the robustness properties of the closed-loop system are analyzed.
PID: Automatic tuning
PID controllers can be tuned automatically by specifying and solving an AutoTuningProblem. See PID Autotuning for more details.
using DyadControlSystems, Plots
P = DemoSystems.double_mass_model()
# Robustness constraints
Ms = 1.3 # Maximum allowed sensitivity function magnitude
Mt = Ms # Maximum allowed complementary sensitivity function magnitude
Mks = 1000.0 # Maximum allowed magnitude of transfer function from process output to control signal, sometimes referred to as noise sensitivity.
w = 2π .* exp10.(LinRange(-2, 2, 200)) # Frequency grid
Ts = 0.005 # Discretization time
Tf = 10 # Simulation time
prob = AutoTuningProblem(; P, Ms, Mt, Mks, w, Ts, Tf, metric = :IE)
res = solve(prob)
plot(res)LQG control
We design an LQR controller using the function lqr
using DyadControlSystems, Plots, LinearAlgebra
P = DemoSystems.double_mass_model()
# Design controller
Q1 = diagm([1000, 1, 1, 1]) # Weighting matrix for state
Q2 = I # Weighting matrix for input
L = lqr(P, Q1, Q2) # Calculate the LQR feedback gain
# Simulation
u(x,t) = -L*x # Input function
x0 = [1, 0, 1.1, 0] # Initial condition
y, t, x, uout = lsim(P, u, 10; x0=x0) # Simulate the system
plot(t, x', lab=["Position m1" "Velocity m1" "Position m2" "Velocity m2"], xlabel="Time [s]", title="LQR control")and a Kalman filter (state observer) using the function kalman. We create the controller object using the function observer_controller
R1 = diagm([10, 10, 100, 100]) # Covariance matrix for state
R2 = I # Covariance matrix for measurement
K = kalman(P, R1, R2) # Calculate the Kalman filter gain
C = observer_controller(P, L, K) # Create the controller statespace object
Gcl = feedback(P*C) # Form the closed-loop system from reference to output
f1 = bodeplot([P*C, Gcl], lab=["PC" "" "PC/(1+PC)" ""]) # We plot the Bode curve of the loop-transfer function and the closed-loop transfer function
f2 = plot(step(Gcl, 0:0.01:10)) # And plot a step response
plot(f1,f2)See LQGProblem for more advanced functionality.
Functions used:
$\mathcal{H}_\infty$ control
We solve $\mathcal{H}_\infty$-design problems using the function hinfsynthesize or hinfsyn_lmi. In the example below, we first create an ExtendedStateSpace object using the function hinfpartition and then solve the design problem using hinfsynthesize. We can plot the specification curves using the function specificationplot.
using DyadControlSystems, Plots, LinearAlgebra
P = DemoSystems.double_mass_model()
# Design controller
WS = makeweight(1e5, 0.1, 0.5) # Sensitivity weight function
WU = ss(1) # Output sensitivity weight function. Increase this value to penalize controller effort more
# Complementary sensitivity weight function
WT = [] # We do not put any weight on T in this example
Pe = hinfpartition(P, WS, WU, WT) # Create an ExtendedStateSpace object
hinfassumptions(Pe) # Not satisfied due to integrators in plant model
Pe.A .-= 1e-6I(Pe.nx) # Move integrating poles slightly into the stable region
hinfassumptions(Pe) # Satisfied
C, γ = hinfsynthesize(Pe, γrel=1.05)
Pcl, S, CS, T = hinfsignals(Pe, P, C)
specificationplot([S, CS, T], [WS, WU, WT], γ)Plot transfer functions and step response
Gcl = feedback(P*C) # We can form the closed-loop system from reference to output using [`feedback`](@ref)
f1 = bodeplot([P*C, Gcl], lab=["PC" "" "PC/(1+PC)" ""]) # We plot the Bode curve of the loop-transfer function and the closed-loop transfer function
f2 = plot(step(Gcl, 0:0.01:10)) # And plot a step response
plot(f1,f2)If you are looking for robust-control functionality, see the section on Robust control.
Functions used:
Linear MPC control
The following example creates a linear MPC controller with quadratic cost function that penalizes outputs. Constraints are used for states and inputs. See Model-Predictive Control (MPC) for more details.
using DyadControlSystems, Plots, LinearAlgebra
using DyadControlSystems.MPC
P = DemoSystems.double_mass_model()
P = c2d(P, 0.01) # Discretize the model
N = 20 # MPC prediction horizon
x0 = [0.0, 0, 0, 0] # Initial condition
r = [1.0] # Output reference
op = OperatingPoint() # Empty operating point implies x = u = y = 0
# Control limits
umin = -5 * ones(P.nu)
umax = 5 * ones(P.nu)
# State limits (state constraints are soft by default)
xmin = -1.2 * ones(P.nx)
xmax = 1.2 * ones(P.nx)
constraints = MPCConstraints(; umin, umax, xmin, xmax)
solver = OSQPSolver(
verbose = false,
eps_rel = 1e-6,
max_iter = 1500,
check_termination = 5,
polish = true,
)
Q1 = Diagonal([1000]) # output cost matrix
Q2 = spdiagm(ones(P.nu)) # control cost matrix
R1 = diagm([10.0, 10, 100, 100]) # Covariance matrix for state
R2 = I(P.nu) # Covariance matrix for measurement
kf = KalmanFilter(ssdata(P)..., R1, R2)
named_sys = named_ss(P, x=[:pos_m1, :vel_m1, :pos_m2, :vel_m2], u=:force, y=:pos_m1) # give names to signals for nicer plot labels
predmodel = LinearMPCModel(named_sys, kf; constraints, op, x0, z=P.C) # z=P.C indicates that we are penalizing the output rather than the state vector
prob = LQMPCProblem(predmodel; Q1, Q2, N, solver, r)
T = 1000 # Simulation length (time steps)
hist = MPC.solve(prob; x0, T, verbose = false)
plot(hist); hline!([umin umax], lab="Constraint", l=(:black, :dash), sp=2)Functions used: