MPC control of a Continuously Stirred Tank Reactor (CSTR)

This tutorial is available as a webinar:

The Continuously Stirred Tank Reactor (CSTR) is a common model for a chemical reactor. The model is available as a demo system in JuliaSimControl.ControlDemoSystems.cstr(), and has the following equations

julia> sys = JuliaSimControl.ControlDemoSystems.cstr();
julia> display(sys.sys)

sys.sys

\[ \begin{align} \frac{\mathrm{d} C_a\left( t \right)}{\mathrm{d}t} =& - 9.043 \cdot 10^{9} e^{\frac{-8560}{273.15 + T_r\left( t \right)}} \left|C_a\left( t \right)\right|^{2} + \left( 5.1 - C_a\left( t \right) \right) F\left( t \right) - 1.287 \cdot 10^{12} C_a\left( t \right) e^{\frac{-9758.3}{273.15 + T_r\left( t \right)}} \\ \frac{\mathrm{d} C_\beta\left( t \right)}{\mathrm{d}t} =& 1.287 \cdot 10^{12} C_a\left( t \right) e^{\frac{-9758.3}{273.15 + T_r\left( t \right)}} - C_\beta\left( t \right) F\left( t \right) - 1.287 \cdot 10^{12} C_\beta\left( t \right) e^{\frac{-9758.3}{273.15 + T_r\left( t \right)}} \\ \frac{\mathrm{d} T_r\left( t \right)}{\mathrm{d}t} =& 30.829 \left( T_k\left( t \right) - T_r\left( t \right) \right) - 0.35563 \left( - 3.7845 \cdot 10^{11} e^{\frac{-8560}{273.15 + T_r\left( t \right)}} \left|C_a\left( t \right)\right|^{2} + 5.4054 \cdot 10^{12} C_a\left( t \right) e^{\frac{-9758.3}{273.15 + T_r\left( t \right)}} - 1.4157 \cdot 10^{13} C_\beta\left( t \right) e^{\frac{-9758.3}{273.15 + T_r\left( t \right)}} \right) + \left( 130 - T_r\left( t \right) \right) F\left( t \right) \\ \frac{\mathrm{d} T_k\left( t \right)}{\mathrm{d}t} =& 0.1 \left( 866.88 \left( - T_k\left( t \right) + T_r\left( t \right) \right) + \textnormal{\.{Q}}\left( t \right) \right) \end{align} \]

The system has 4 states and 2 inputs and strongly nonlinear dynamics, in particular, if the reaction $C_A \rightarrow C_B$ taking place is exothermic, a higher reactor temperature $T_r$ causes a further increased reaction rate, causing a condition called temperature runaway, i.e., the system is unstable. In this tutorial, we will design a nonlinear MPC controller that controls the steady-state concentration of one of the reactants, reactant $C_B$, while keeping all state components within safe operating limits.

A depiction of a CSTR is shown below, a motor is continuously stirring the reactor contents, so we may safely assume that the contents are well mixed and the whole take has a homogenous temperature and concentration distribution.

The variables available for us to manipulate are the feed $F$ of reactant $A$, and the heat flow $Q̇$ from the cooling jacket.

The structure sys returned from the cstr contains a some useful information that we will unpack for later use. We will also specify the initial state of the system x0, the reference r and the MPC prediction horizon N:

using StaticArrays
dynamics = sys.dynamics
nu  = dynamics.nu # number of controls
nx  = dynamics.nx # number of states
Ts  = sys.Ts # sample time
x0  = [0.8, 0.5, 134.14, 130] # Initial state
u0  = [10, -1000]
r   = SA[NaN, 0.6, NaN, NaN]
N   = 30 # MPC prediction horizon

The reference r can be anything really, it does not have to be an array of the same length as the number of states. We select it as such an array though and indicate that we only have a reference for one of the states and do not really care about the other states.

For improved numerics, we specify scaling vectors that indicate the typical ranges for states and inputs. This will help the solver select reasonable tolerances for convergence of the dynamics constraints.

scale_x = [1, 1, 100, 100]
scale_u = [100, 2000]

For simulation purposes, we discretize the dynamics using RK4 (rk4), we also specify that we want to use the default parameters:

discrete_dynamics = MPC.rk4(dynamics, Ts)

p = sys.p # A NamedTuple of parameters for this system is available in sys.p

(K0_ab = 1.287e12, K0_bc = 1.287e12, K0_ad = 9.043e9, R_gas = 0.00831446, E_A_ab = 9758.3, E_A_bc = 9758.3, E_A_ad = 8560.0, Hᵣ_ab = 4.2, Hᵣ_bc = -11.0, Hᵣ_ad = -41.85, Rou = 0.9342, Cp = 3.01, Cpₖ = 2.0, Aᵣ = 0.215, Vᵣ = 10.0, m_k = 5.0, T_in = 130.0, K_w = 4032.0, C_A0 = 5.1)

Creating constraints

The system has a number of constraints on inputs and states that the MPC controller must respect, those are given in

sys.lb

6-element StaticArraysCore.SizedVector{6, Pair{Symbolics.Num, Float64}, Vector{Pair{Symbolics.Num, Float64}}} with indices SOneTo(6):
 Cₐ(t) => 0.1
 Cᵦ(t) => 0.1
 Tᵣ(t) => 50.0
 Tₖ(t) => 50.0
  F(t) => 5.0
  Q̇(t) => -8500.0

sys.ub

6-element StaticArraysCore.SizedVector{6, Pair{Symbolics.Num, Float64}, Vector{Pair{Symbolics.Num, Float64}}} with indices SOneTo(6):
 Cₐ(t) => 2.0
 Cᵦ(t) => 2.0
 Tᵣ(t) => 142.0
 Tₖ(t) => 140.0
  F(t) => 100.0
  Q̇(t) => 0.0

We can create constraint objects for the MPC controller like this, the StageConstraint constructor expects a function that defines the constrained output, as well as vectors with the lower and upper bounds of the constrained output. Here, we have simple bounds constraints on the variables, but we could have used any nonlinear function of states and inputs in our constrain if we would have liked to.

lb = [0.1, 0.1, 50, 50, 5, -8500]
ub = [2, 2, 140, 140, 100, 0.0]
stage_constraints = StageConstraint(lb, ub) do si, p, t
    SA[
        si.x[1]
        si.x[2]
        si.x[3]
        si.x[4]
        si.u[1]
        si.u[2]
    ]
end

When the constraints are simple bounds constraints on states and control inputs, we do not have to use the generic StageConstraint, and may instead use the simpler BoundsConstraint. Many optimization solvers can handle bounds constraints on variables extra efficiently, so we will use this approach in this tutorial.

xmin = [0.1, 0.1, 50, 50]
xmax = [2, 2, 142, 140]
umin = [5, -8500]
umax = [100, 0.0]
bounds_constraints = BoundsConstraint(; xmin, xmax, umin, umax)

BoundsConstraint{Vector{Float64}}([0.1, 0.1, 50.0, 50.0], [2.0, 2.0, 142.0, 140.0], [5.0, -8500.0], [100.0, 0.0], [0.1, 0.1, 50.0, 50.0], [2.0, 2.0, 142.0, 140.0], [-Inf, -Inf], [Inf, Inf])

The BoundsConstraint allows for a separate constraint to be applied to the terminal state $x(N+1)$, making it extra efficient to implement simple terminal-set constraints.

Creating an objective

The control objective is to regulate the concentration of reactant $C_B$ to , we indicate that with a square penalty on the control error:

running_cost = StageCost() do si, p, t
    abs2(si.x[2]-si.r[2])
end

We may also penalize the control-signal derivative (difference) by using a DifferenceCost. This constructor wants two functions, one that computes the cost based on a difference e, and one function, here called getter, that outputs the signal that we want to compute the difference of, in this case the control inputs $u_1, u_2$. The effect of this is that we penalize $\Delta u = u(k) - u(k-1)$ (if getter is not provided, the default is to get the control signal like we do here). For improved convergence properties, we also include a terminal cost, causing the controller to in optimization work hard to find a trajectory that ends up in the desired state. (We could also force the optimizer to end up in a terminal set, for this, we would have used TerminalStateConstraint.) We package all our cost functions in an Objective.

getter = (si,p,t)->SA[si.u[1], si.u[2]]
difference_cost = DifferenceCost(getter) do e, p, t
    0.005*(0.1/100*abs2(e[1]) + 1e-3/2000*abs2(e[2]) )# Control action penalty should be on differences
end

terminal_cost = TerminalCost() do ti, p, t
    abs2(ti.x[2]-ti.r[2])
end

objective = Objective(running_cost, difference_cost, terminal_cost)

Create objective input

Next up, we define an instance of the type ObjectiveInput. This structure allow the user to pass in an initial guess for the optimal solution from the starting state. To provide such a trajectory, we simulate the system forward in time from the initial condition x0 using the function MPC.rollout, here, we make use of the discretized dynamics.

x = zeros(nx, N+1) .+ x0
u = randn(nu, N)
x, u = MPC.rollout(discrete_dynamics, x0, u, p, 0)
oi = ObjectiveInput(x, u, r)

Create observer solver and problem

The MPC framework requires the specification of an observer that is responsible for feeding (an estimate of) the state of the system into the optimization-part of the MPC controller. In this example, we use the StateFeedback, which is so named due to it not relying on measurements, rather, it knows the state of the system from the simulation model.

We also define the solver we want to use to solve the optimization problems. We will make use of IPOPT in this example, a good general-purpose solver.

solver = MPC.IpoptSolver(;
        verbose                     = false,
        tol                         = 1e-6,
        acceptable_tol              = 1e-3,
        max_iter                    = 500,
        max_cpu_time                = 20.0,
        max_wall_time               = 20.0,
        constr_viol_tol             = 1e-6,
        acceptable_constr_viol_tol  = 1e-3,
        acceptable_iter             = 5,
        exact_hessian               = true,
        acceptable_obj_change_tol   = 0.01,
)

observer = StateFeedback(discrete_dynamics, x0)

Next up, we define the transcription scheme we want to use when transcribing the infinite-dimensional continuous-time problem to a finite-dimensional discrete-time problem. In this example, we will use CollocationFinE with 2 collocation points, a method suitable for stiff dynamics.

disc = CollocationFinE(dynamics, false; n_colloc=2, scale_x)

We are now ready to create the GenericMPCProblem structure. We provide scale_x when creating the MPC problem so that the solver will scale the dynamics constraints using the typical magnitude of the state components. This may improve the numerical performance in situations where different state components have drastically different magnitudes, which is the case for this system.

prob = GenericMPCProblem(
    dynamics;
    N,
    observer,
    objective,
    constraints = [bounds_constraints],
    p,
    Ts,
    objective_input = oi,
    solver,
    xr = r,
    presolve = true,
    scale_x,
    scale_u,
    disc,
    verbose = false,
)

Run MPC controller

We may now simulate the MPC controller using the function MPC.solve. We provide the discretized dynamics dyn_actual=discrete_dynamics as our simulation model (may not be the same as the prediction model in the MPC controller, which in this case is using the continuous-time dynamics).

history = MPC.solve(prob; x0, T = 50, verbose = false, dyn_actual = discrete_dynamics)
plot(history, layout=(3, 2), sp=[1 2 3 4 1 2 3 4 5 6], title="", xlabel="Time [hrs]", topmargin=-5Plots.mm)
hline!(xmax[3:4]', ls=:dash, lw=1, color=:black, sp=(3:4)', lab="Upper bound")

The result should indicate that the state $C_B$ converges to the reference, while the reactor is operating within the safe temperature limits specified by the constraints.

Enter uncertainty

What would happen if the plant model does not exactly match reality? We could simulate the effect of a model mismatch in one or several of the parameters by supplying a different parameter for the actual dynamics. Below, we simulate that the actual activation energy for the reaction is 5% lower than the nominal value. This will result in a higher reaction rate, and thus a higher temperature in the reactor.

p_actual = Base.setindex(p, 0.95*p.E_A_ad, :E_A_ad) # Decrease E_A_ad by 5%
history_u = MPC.solve(prob; x0, T = 50, verbose = true, dyn_actual = discrete_dynamics, p_actual);
plot(history_u, layout=(3, 2), sp=[1 2 3 4 1 2 3 4 5 6], title="", xlabel="Time [hrs]", topmargin=-5Plots.mm)
hline!(xmax[3:4]', ls=:dash, lw=1, color=:black, sp=(3:4)', lab="Upper bound")

This time, both temperatures exceed the safe operating bounds, and the state $C_β$ does not converge to the reference!

Robust MPC

If we have parameter uncertainty in the system, we can opt to design a robust MPC controller. Below, we model a ±5% uncertainty in the $E_{A_ad}$ coefficient, and design a robust MPC controller that will operate within the safe operating bounds even if the actual value of $E_{A_ad}$ is outside the nominal range. For a more detailed introduction to robust MPC, see the Robust MPC with uncertain parameters tutorial. The code below creates the uncertain parameter set p_uncertain, and then creates a robust MPC problem with a robust horizon of 1. For insight into how the robust controller works, we animate the predictions it makes as it solves the optimization problem at each time step.

p_uncertain = MPCParameters.([
    p, # nominal case
    Base.setindex(p, 0.94*p.E_A_ad, :E_A_ad), # 6% lower (some tolerance is beneficial)
    Base.setindex(p, 1.06*p.E_A_ad, :E_A_ad), # 6% higher
])
observer = StateFeedback(discrete_dynamics, x0)
prob_robust = GenericMPCProblem(
    dynamics;
    N,
    observer,
    objective,
    constraints = [bounds_constraints],
    p = p_uncertain,
    Ts,
    objective_input = oi,
    solver,
    xr = r,
    presolve = true,
    scale_x,
    scale_u,
    disc,
    verbose = true,
    robust_horizon = 1, # Indicate that we are designing a robust MPC controller
)

anim = Plots.Animation()
function callback(actual_x, u, x, X, U)
    n_robust = length(p_uncertain)
    (; nx, nu) = dynamics
    T = length(X)
    tpast = 1:T
    fig = plot(
        tpast,
        reduce(hcat, X)',
        c       = 1,
        layout  = (3,2),
        sp      = (1:nx)',
        ylabel  = permutedims(state_names(dynamics)),
        legend  = true,
        lab     = "History",
        xlims   = (1,60),
        size    = (600, 800),
    )
    plot!(
        tpast,
        reduce(hcat, U)',
        c       = 1,
        sp      = (1:nu)' .+ nx,
        ylabel  = permutedims(input_names(dynamics)),
        legend  = true,
        lab     = "History",
        xlims   = (1,60),
    )

    xs = map(1:n_robust) do ri
        xu, uu = get_xu(prob_robust, ri)
        xu
    end
    Xs = reduce(vcat, xs)
    tfuture = (1:size(Xs, 2)) .+ (T - 1)
    lab = ""
    plot!(tfuture, Xs'; c = (1:n_robust)', l = :dash, sp = (1:nx)', lab)

    us = map(1:n_robust) do ri
        xu, uu = get_xu(prob_robust, ri)
        uu
    end
    Us = reduce(vcat, us)
    tfuture = (1:size(Us, 2)) .+ (T - 1)
    plot!(tfuture, Us'; c = (1:n_robust)', l = :dash, sp = (1:nu)'.+ nx, lab)
    hline!(xmax[3:4]', l = (:gray, :dash), sp=(3:4)', lab="Upper bound")
    hline!([r[2]], l = (:green, :dash), lab = "Reference", sp=2)
    Plots.frame(anim, fig)
end

history_robust = MPC.solve(prob_robust; x0, T = 50, verbose = false, dyn_actual = discrete_dynamics, p_actual, callback);
gif(anim, fps = 15)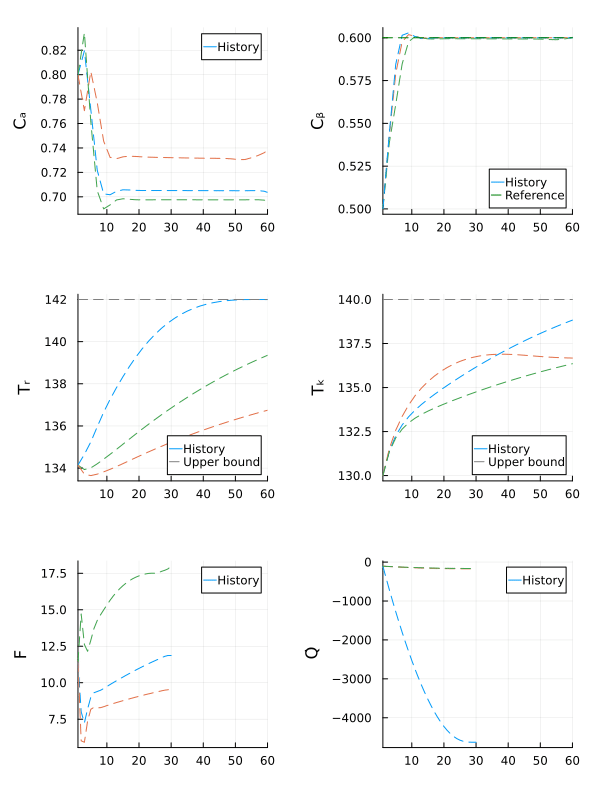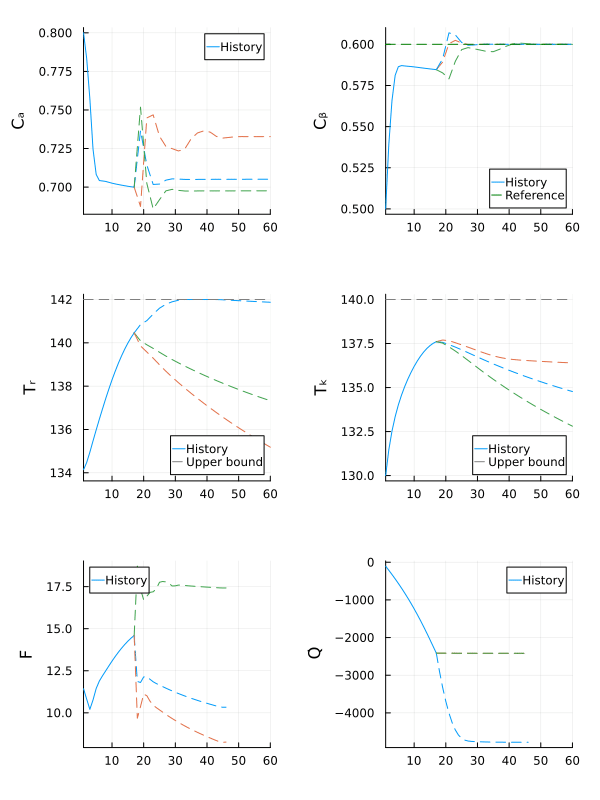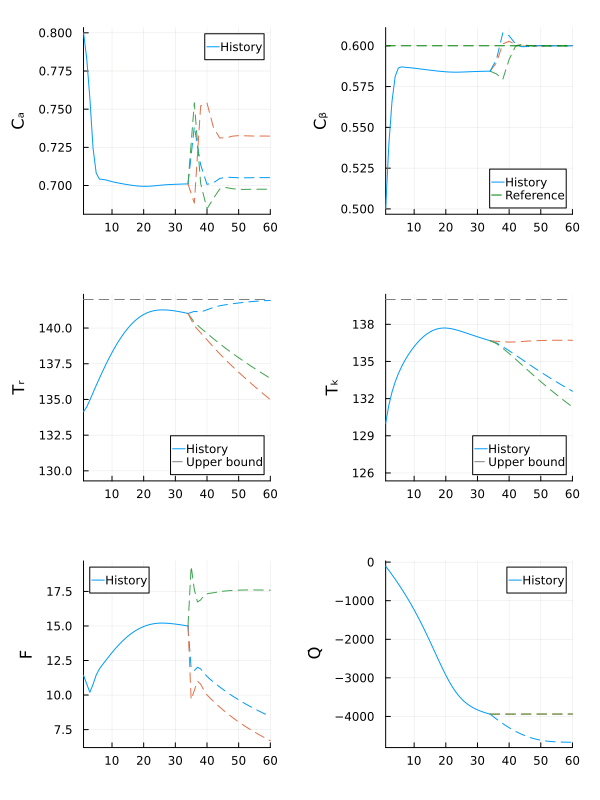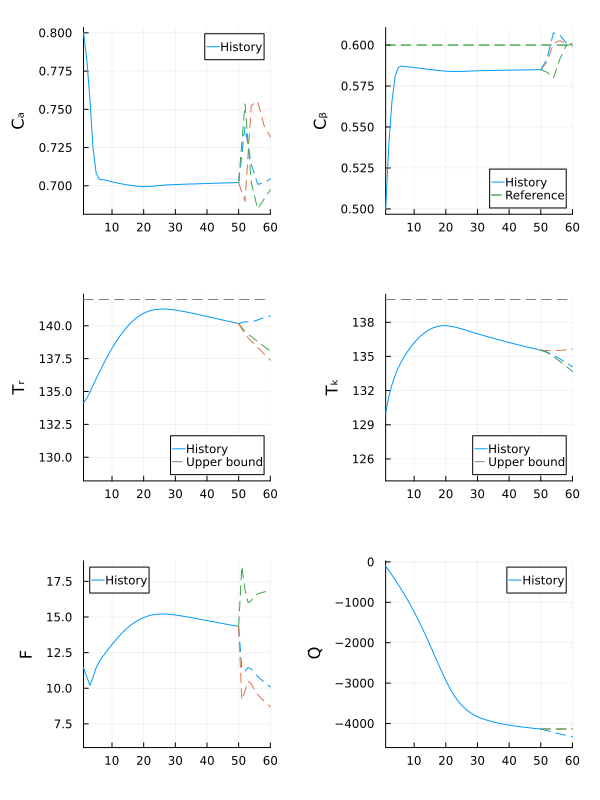

The robust MPC controller manages to make the state $C_β$ converge close to the reference, while keeping all other states within the safe operating bounds, even if the actual value of $E_{A_ad}$ is outside the nominal range.

We can plot the final trajectory like before:

plot(history_robust, layout=(3, 2), sp=[1 2 3 4 1 2 3 4 5 6], title="", xlabel="Time [hrs]", topmargin=-5Plots.mm)
hline!(xmax[3:4]', l = (:gray, :dash), lab = "Upper bound", sp=[3 4])

In this case, the controller does not meet the reference exactly, but it does the best it can while making sure to respect the state constraints for any realization of the uncertain plant.

Summary

This tutorial has demonstrated the use of constrained nonlinear MPC by means of the GenericMPCProblem structure on a highly nonlinear MIMO system using collocation on finite elements transcription. We ended the tutorial by designing a robust MPC controller that could tolerate uncertainty in plant dynamics. An alternative approach to designing a robust controller is to design an adaptive controller, see Adaptive MPC for an example.

using Test
@test history.X[end][2] ≈ r[2] rtol=1e-3
@test history_robust.X[end][2] ≈ 0.6 atol = 0.02
@test all(<=(xmax[3]), getindex.(history_robust.X, 3))
@test all(<=(xmax[4]), getindex.(history_robust.X, 4))

Test Passed