MPC for autonomous lane changes
In this example, we will develop a lane-changing controller using Model-Predictive Control (MPC). We will use a dynamical model of the car that is sometimes referred to as the kinematic bicycle model, given by the following equations
\[\begin{aligned} \dot{x} &= v \cos(\psi) \\ \dot{y} &= v \sin(\psi) \\ \dot{v} &= a \\ \dot{\psi} &= \frac{v}{L} \tan(\delta) \end{aligned}\]
Where $x, y$ are positional coordinates, $\psi$ is the orientation, $v$ is the velocity, $\delta$ is the steering angle, and $a$ is the acceleration. The parameter $L$ is the distance between the front and rear wheels. The state of the car is given by the vector $\mathbf{x} = [x, y, v, \psi]^T$ and the control input is given by $\mathbf{u} = [a, \delta]^T$. When we solve the control problem, we omit the $x$ coordinate, and only consider the lateral position on the road, $y$, as well as the velocity.
After having loaded the necessary packages
using JuliaSimControl
using JuliaSimControl.MPC
using TrajectoryLimiters
using Plots, StaticArraysPlots.GRBackend()we generate a reference trajectory for the lateral position y with bounded velocities and accelerations. For this, we make use of the TrajectoryLimiters package, that provides a nonlinear filter to post-process a primitive reference trajectory such that the filtered trajectory has bounded velocities and accelerations.
ẍM = 0.4 # Maximum lateral acceleration
ẋM = 1.5 # Maximum velocity
Ts = 0.1 # Sample time
traj(t) = 1.5 * sign(sin(2pi * t / 20)) # Reference to be smoothed
t = 0:Ts:30 # Time vector
R = traj.(t) # An array of sampled position references
limiter = TrajectoryLimiter(Ts, ẋM, ẍM)
Y, Ẏ, Ÿ = limiter(R)
plot(
t,
[Y Ẏ Ÿ],
plotu = true,
c = :black,
title = ["Lateral position \$y(t)\$" "Lateral velocity \$\\dot{y}(t)\$" "Lateral acceleration \$\\ddot y(t)\$"],
ylabel = "",
lab = "",
layout = (3, 1),
)
plot!(traj, extrema(t)..., sp = 1, lab = "Raw reference", l = (:black, :dashdot))
We now define the dynamics and specify that we can measure all three states, $y, v, ψ$.
function car_dynamics(x, u, p, t)
y, v, ψ = x
a, δ = u
L = 2.9 # Length between the axels
ẏ = v * sind(ψ)
v̇ = a
ψ̇ = v / L * tand(δ)
return SA[ẏ, v̇, ψ̇]
end
measurement = (x, u, p, t) -> x
nx = 3 # Number of states
nu = 2 # Number of inputs
ny = 3 # Number of outputs
# Names for states and inputs
xn = [:y, :v, :ψ]
un = [:a, :δ]
yn = xn
cont_dynamics = FunctionSystem(car_dynamics, measurement; x = xn, u = un, y = yn)When we discretize the dynamics, we will use a time step of $T_s = 0.1$ seconds. The discrete dynamics is required for simulation purposes, while the MPC controller will internally use Trapezoidal integration in this example.
Ts = 0.1
discrete_dynamics = MPC.rk4(cont_dynamics, Ts)
p = nothingNext up, we define an initial condition $x_0$, the reference trajectory $x_r$ that includes our lateral reference generated above, as well as bounds for the state and inputs. We'll limit the velocity to 120km/h (and divide by 3.6 to get m/s), the acceleration to be within $[-10, 0.2g]$ m/s² and the steering angle to be within $[-25, 25]°$. We also define scaling factors scale_x, scale_u for improved numerics.
x0 = [ # initial state
0, # y
30 / 3.6, # v
0, # ψ
]
xr = [ # reference trajectory
Y' # y
fill(50 / 3.6, 1, length(Y)) # v
fill(0, 1, length(Y)) # ψ
]
# Control limits
umin = [
-10, # a
-25, # δ
]
umax = [0.2 * 9.8, 25]
# State limits
xmin = [
-1.53, # y
0, # v
-6, # ψ
]
xmax = [
1.53, # y
120 / 3.6, # v
6, # ψ
]
scale_x = [
10, # y
30, # v
60.0, # ψ
]
scale_u = [120 / 3.6, 60.0]
bounds_constraints = BoundsConstraint(; xmin, xmax, umin, umax)The cost function will be quadratic and we will penalize the deviation from the reference trajectory. We will also penalize the control inputs $u$ to avoid large accelerations and steering angles, and control input differences $\Delta u$ to avoid high jerk (high jerk causes neck discomfort).
running_cost = StageCost() do si, p, t
abs2(si.x[1] .- si.r[1]) + # y
0.02abs2(si.x[2] .- si.r[2]) + # v
0.01abs2(si.x[3] .- si.r[3]) + # ψ
0.01si.u[1]^2 + # a
0.00001si.u[2]^2 # δ
end
# Penalize control-action differences
getter = (si,p,t)->SA[si.u[1], si.u[2]] # This function picks the signals to compute the difference of
difference_cost = DifferenceCost(getter) do e, p, t
abs2(e[1]) + # a
0.001abs2(e[2]) # δ
end
objective = Objective(running_cost, difference_cost)To improve the stability properties of our MPC controller, we make use of a TerminalStateConstraint that enforce the final state to be equal to the reference state.
terminal_constraint = TerminalStateConstraint(zeros(1), zeros(1)) do ti, p, t
ti.x[1] - ti.r[1]
endTerminalStateConstraint{Main.var"#9#10", Vector{Float64}}(Main.var"#9#10"(), [0.0], [0.0])We also define an instance of ObjectiveInput that can be used to set the initial guess for the optimizer, as well as the prediciton horizon $N$. In this case, we will simply use a random guess.
N = 30
x = zeros(nx, N + 1) .+ x0
u = randn(nu, N)
x, u = MPC.rollout(discrete_dynamics, x0, u, p, 0)
oi = ObjectiveInput(x, u, xr)To solve the problem, we will use the IPOPT solver with Trapezoidal discretization
solver = MPC.IpoptSolver(;
verbose = false,
tol = 1e-6,
acceptable_tol = 1e-2,
max_iter = 5000,
max_cpu_time = 20.0,
max_wall_time = 20.0,
constr_viol_tol = 1e-6,
acceptable_constr_viol_tol = 1e-3,
acceptable_iter = 5,
exact_hessian = true,
mu_init = 1e-6,
acceptable_obj_change_tol = 0.01,
)
observer = StateFeedback(discrete_dynamics, x0) # This indicates that we have perfect knowledge of the states
disc = Trapezoidal(cont_dynamics)We are now ready to construct the GenericMPCProblem
prob = GenericMPCProblem(
cont_dynamics;
N,
Ts,
observer,
objective,
constraints = [bounds_constraints, terminal_constraint],
p,
objective_input = oi,
solver,
xr,
presolve = true,
scale_x,
scale_u,
jacobian_method = :symbolics,
disc,
verbose = true,
)[ Info: Building constant Hessian function
[ Info: Calculating sparse Jacobian
[ Info: Done
[ Info: Building symbolic constraint Jacobian
[ Info: Building sparse lagrangian Hessian
[ Info: Done
[ Info: Testing loss function
[ Info: Testing gradient function
[ Info: Testing hessian function
[ Info: Testing constraint function
[ Info: Testing constraint jacobian function
[ Info: Testing lagrangian hessian function
[ Info: Done testing
[ Info: Presolving for initial trajectoryBefore we solve the problem, we will define a callback function with which we can create a little animation of the signals as the optimization progresses.
anim = Plots.Animation()
function callback(actual_x, u, x, X, U)
T = length(X)
tpast = 1:T
tfuture = (1:size(x, 2)) .+ (T - 1)
fig = plot(
tpast,
reduce(hcat, X)',
c = (1:nx)',
layout = (3, 1),
sp = (1:3)',
title = ["Lateral position \$y(t)\$" "Velocity \$v(t)\$" "Angle \$ψ(t)\$"],
ylabel = "",
legend = true,
lab = "History",
)
plot!(tfuture, x', c = (1:nx)', l = :dash, sp = (1:3)', lab = "Prediction")
plot!(
tfuture,
prob.xr[:, 1:length(tfuture)]',
c = :black,
l = :dot,
sp = (1:3)',
lab = "Reference",
)
Plots.frame(anim, fig)
end
history = MPC.solve(prob; x0, T = 300, dyn_actual = discrete_dynamics, callback);
gif(anim, "/tmp/selfdriving.gif", fps = 25)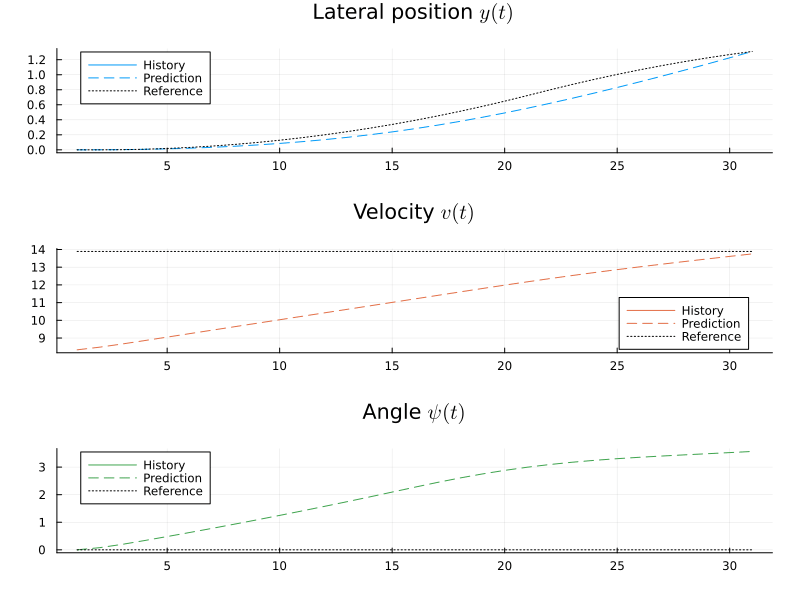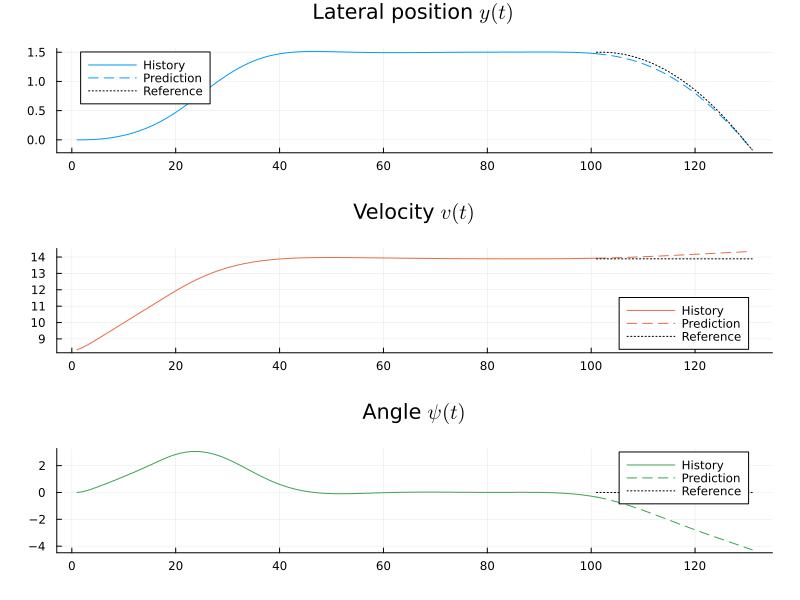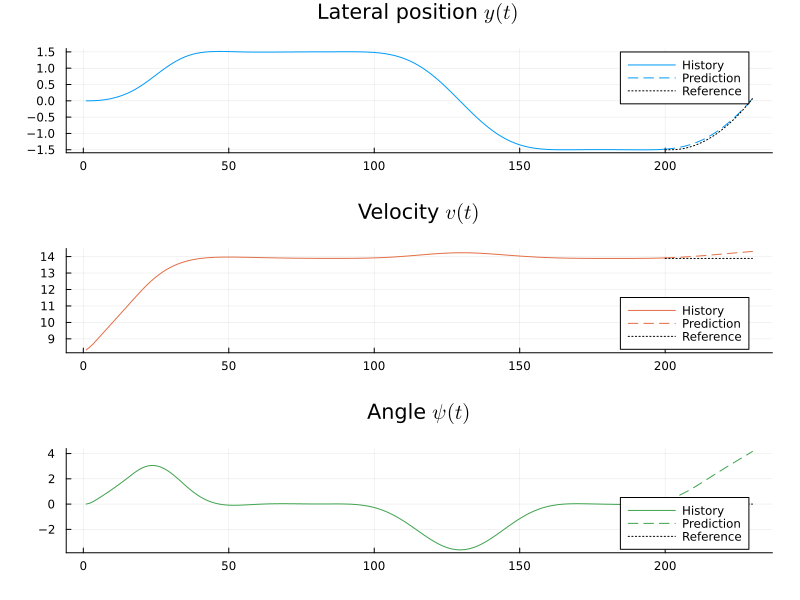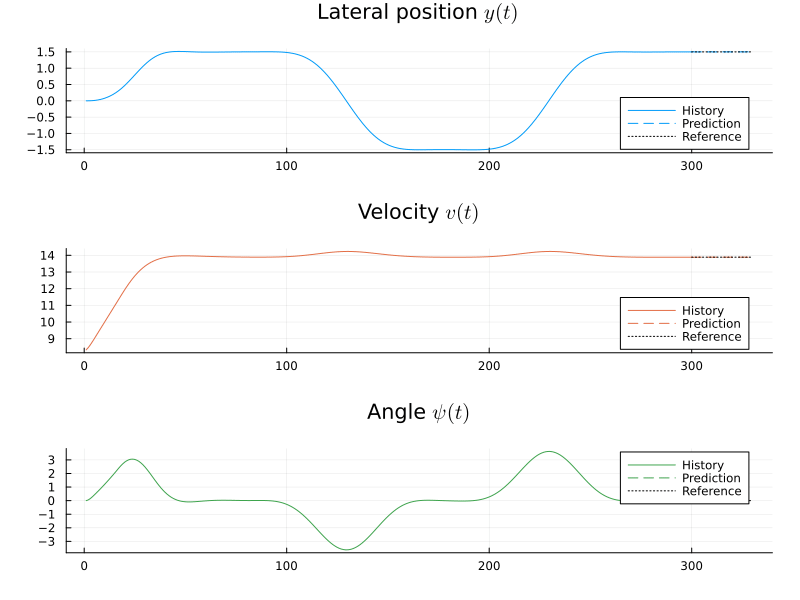
We can also plot the result in a more traditional way
X,E,R,U,_ = reduce(hcat, history)
fx = plot(X', layout=nx, lab=permutedims(state_names(cont_dynamics)))
plot!(R', lab=permutedims(state_names(cont_dynamics)) .* "ᵣ", l=(:black, :dash))
plot(
fx,
plot(U', layout=nu, lab=permutedims(input_names(cont_dynamics))),
)
Finally, we produce a little animation of the car changing lanes. To get the $x$ coordinate which we did not solve for with the MPC controller, we redefine the dynamics to include this as well
function animation_dynamics(x, u, p, t)
x, y, v, ψ = x
a, δ = u
L = 2.9 # Length between the axels
ẋ = v * cosd(ψ)
ẏ = v * sind(ψ)
v̇ = a
ψ̇ = v / L * tand(δ)
return [ẋ, ẏ, v̇, ψ̇]
end
let
dyn = MPC.rk4(animation_dynamics, Ts)
x = [0; x0]
Xanim = [x]
anim = Plots.Animation()
x_coords = [-1, 1, 1, -1, -1]
y_coords = 0.2*[-1, -1, 1, 1, -1]
car = Shape(x_coords, y_coords)
for i in 1:size(U, 2)
u = U[:, i]
x = dyn(x, u, p, i)
push!(Xanim, x)
fig = plot(first.(Xanim), getindex.(Xanim, 2),
ylabel = "",
legend = false,
lab = "History",
ylims = (-2.3, 2.3),
xlims = (-1, size(U, 2)),
size = (1300, 120),
framestyle = :none,
)
hline!([-0.75 0.75], c = :black, l = :dash, primary=false)
hline!([-2.25 2.25], c = :black, primary=false)
cari = Plots.rotate(car, deg2rad(x[4]))
cari = Plots.translate(cari, x[1], x[2])
plot!(cari)
frame(anim, fig)
end
gif(anim, "/tmp/selfdriving_car.gif", fps = 25)
end
This concludes the example!
using Test
@test sum(abs, E[1, :])/size(E, 2) < 0.1
@test sum(abs, E[2, 50:end])/size(E, 2) < 0.5Test Passed