This guide describes how to get started using pre-built models and chemistries from JuliaSimBatteries.jl.
To use JuliaSimBatteries, follow the instructions on setting up the JuliaSim IDE on the JuliaHub Cloud platform. JuliaSimBatteries is unavailable for local installation through the JuliaHub registry.
Creating a battery
The first step is to generate a cell. We can use the pseudo-2D Doyle-Fuller-Newman model by evaluating DFN with the desired chemistry. Here, we use the lithium cobalt oxide (LCO) chemistry.
using JuliaSimBatteries
cell = DFN(LCO())Multiple cathode chemistries are available, including
LCO(lithium cobalt oxide)NMC(lithium nickel manganese cobalt oxide)NCA(lithium nickel cobalt aluminum oxide)LFP(lithium iron phosphate)
Packs and modules
A battery pack is created by connecting multiple batteries in series and parallel. To create a pack, we can use the connection keyword argument to the DFN function. Here, we create a pack with 2 cells in series and 3 cells in parallel.
pack = DFN(LCO(); connection = Pack(series = 2, parallel = 3))Simple discharge experiment
To run a simple experiment on the cell, we can use the solve function. The first argument is cell created above, and the second argument is the type of experiment we want to run. Here, we run a discharge experiment at a C-rate of 1C. C-rate is a measure of the current relative to the capacity of the battery, where 1C fully discharges a battery in 60 minutes and a C-rate of 2C fully discharges a battery in 30 minutes. A default initial state of charge (SOC) is given in the function for the LCO chemistry, and we can override that by passing in a value for SOC_initial.
sol = solve(cell, discharge(1C); SOC_initial = 1)The output of the simulation sol contains the time series of the states of the battery. We can plot the voltage of the battery using the plot function. We can access the states by indexing sol, such as
sol["voltage"]The available states can be accessed by evaluating getstates on the cell
getstates(cell)and plotted using the Plots package
using Plots
plot(sol, "voltage")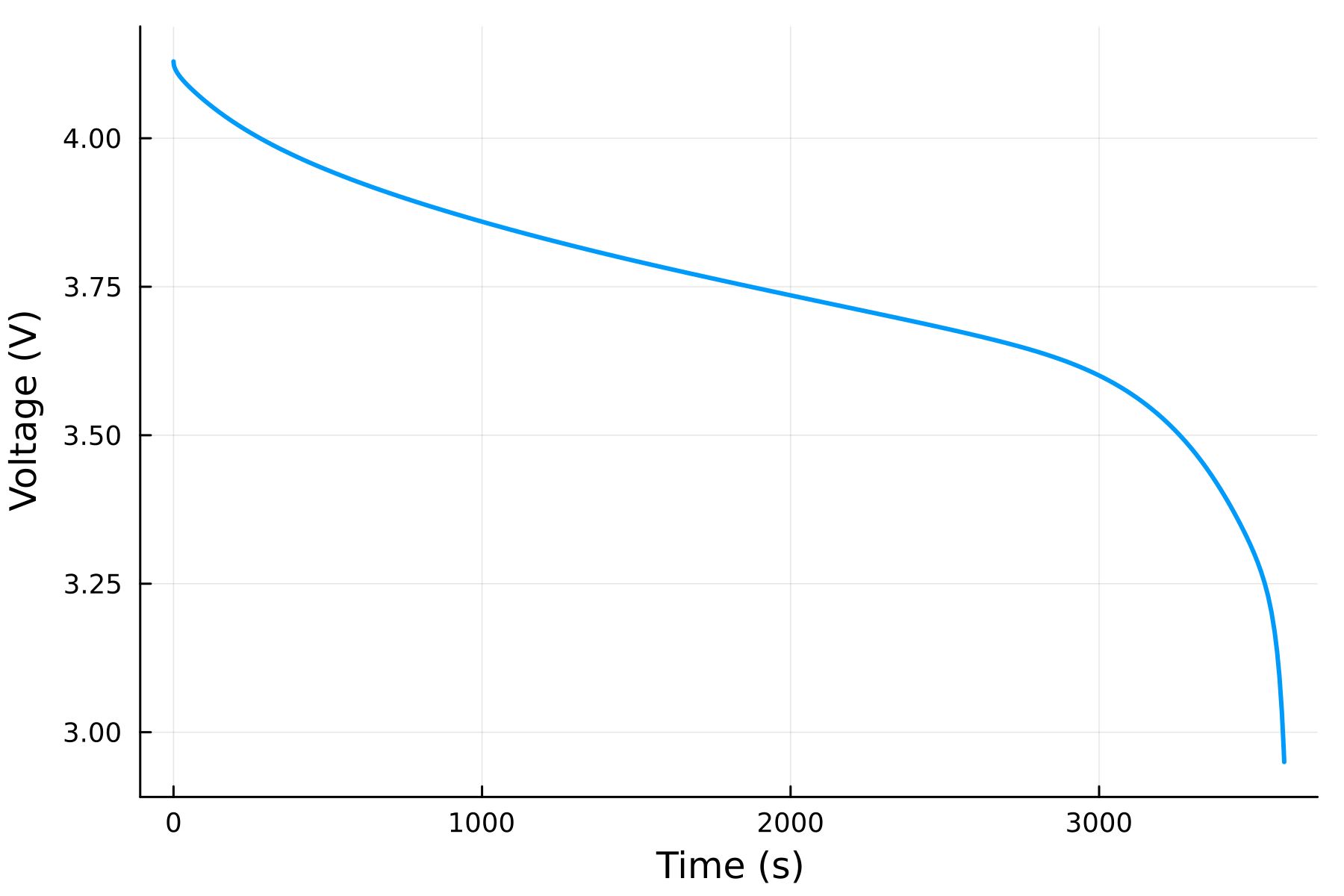
Multi-step charge
Oftentimes, we want to run a series of consecutive experiments on a battery. For example, we may want to charge a battery at a constant current until it reaches a certain voltage, then hold it at that voltage. We can do this by passing in a vector of experiments to the solve function. Here, we charge the battery at 100 A until it reaches 4.2 V, then hold it at that voltage for 300 seconds.
using JuliaSimBatteries, Plots
cell = DFN(LCO())
experiments = [
charge(100; bounds = "total voltage maximum" => 4.2)
voltage(4.2; time = 300)
]
sol = solve(cell, experiments; SOC_initial = 0)
plot(
plot(sol, "current"),
plot(sol, "voltage"),
layout = (:, 1), width = 3, size = (600, 400), dpi = 300
)By convention, charging is denoted by currents with a negative sign and discharging with a positive sign. The voltage function takes a keyword argument time that specifies how long to hold the voltage at the specified value, or until a constraint is activated.
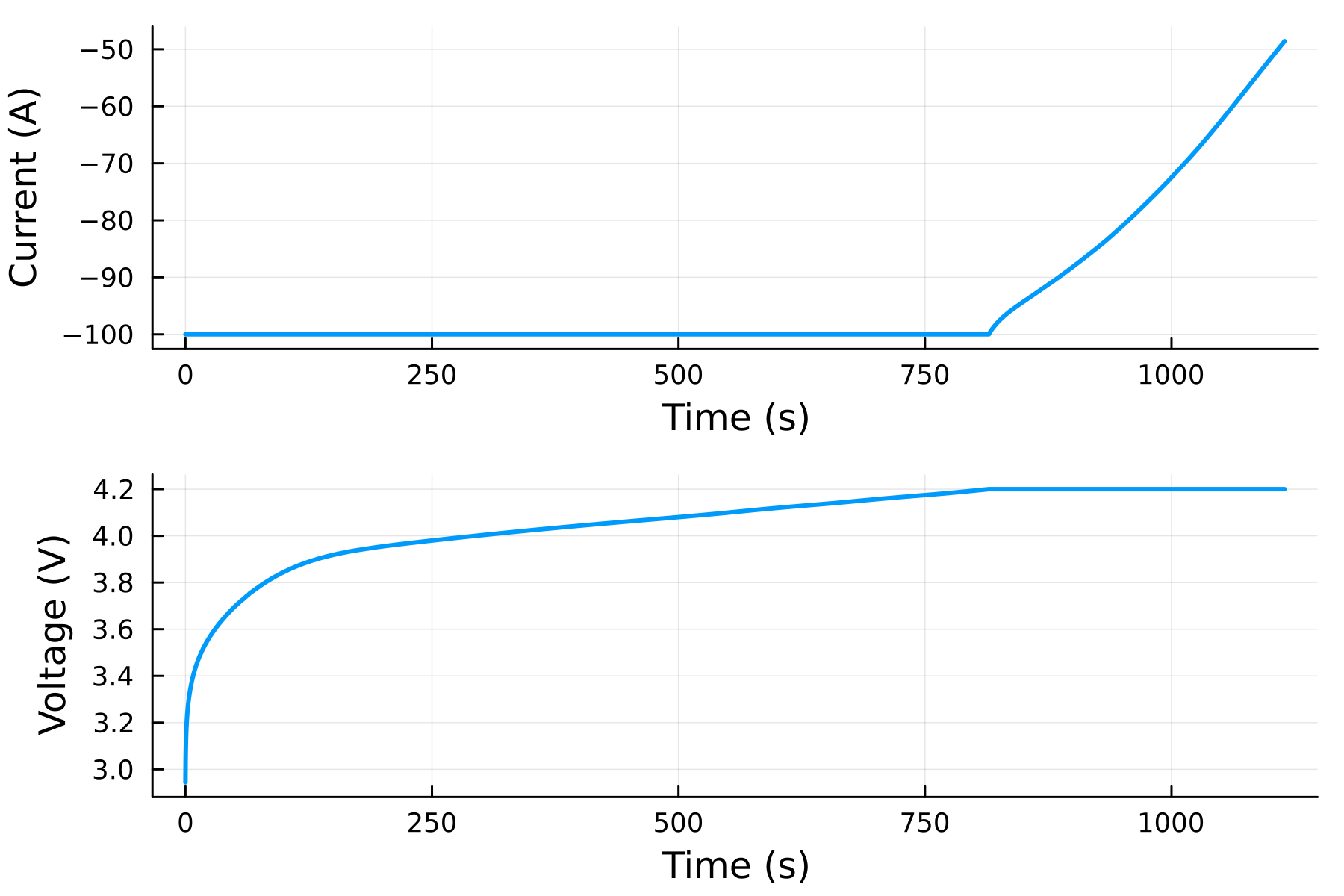
A list of available experiments is given below. The first input to the current and power functions must have the correct sign for the experiment. For example, if we want to discharge at 100 A. If the unit is not specified, the default unit is the SI base unit. Rest does not take an input, but the time must be specified using the keyword argument time.
Lifetime simulation
We can also run a series of experiments to simulate multiple charge and discharge cycles. A discharge cycle is added to the experiments array of the previous example with 1 hour intermittent rest periods. The repeat function is used to repeat the experiments for 350 cycles.
using JuliaSimBatteries, Plots, Unitful
cell = DFN(LCO())
# Set the heat transfer coefficients at the current collectors
setparameters(cell, (
"ambient_1 heat_transfer_coefficient" => 1,
"ambient_2 heat_transfer_coefficient" => 1,
))
# Disable the bounds on the state of charge
setbounds(cell, (
"total state of charge minimum" => NaN,
"total state of charge maximum" => NaN,
))
one_cycle = [
# CC-CV charge
charge(4C)
voltage(:hold)
# rest
rest(time = 3600)
# C/2 discharge
discharge(C/2)
# rest
rest(time = 3600)
]
cycle_count = 350
experiments = repeat(one_cycle, cycle_count)
sol = solve(cell, experiments, SOC_initial = 0)
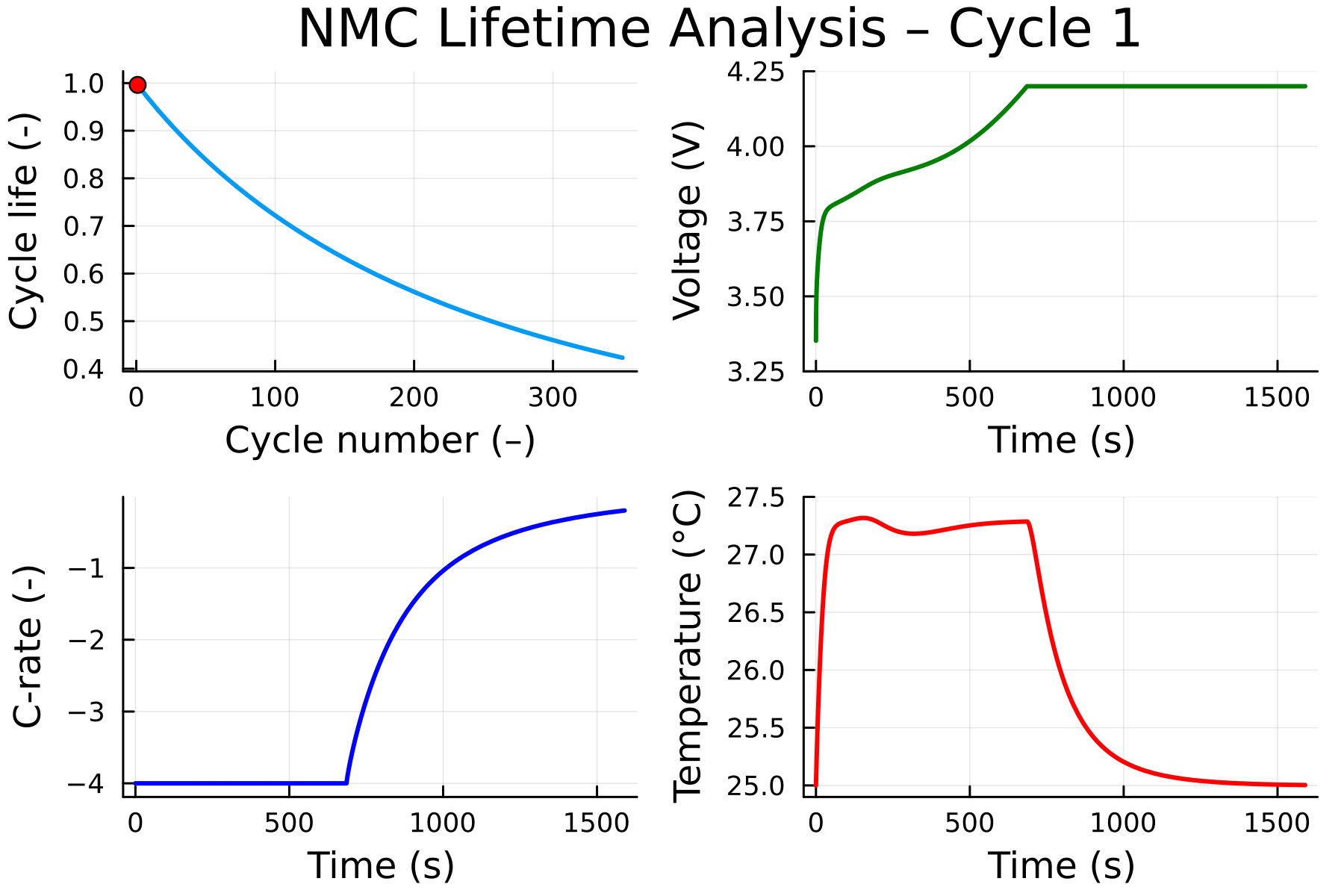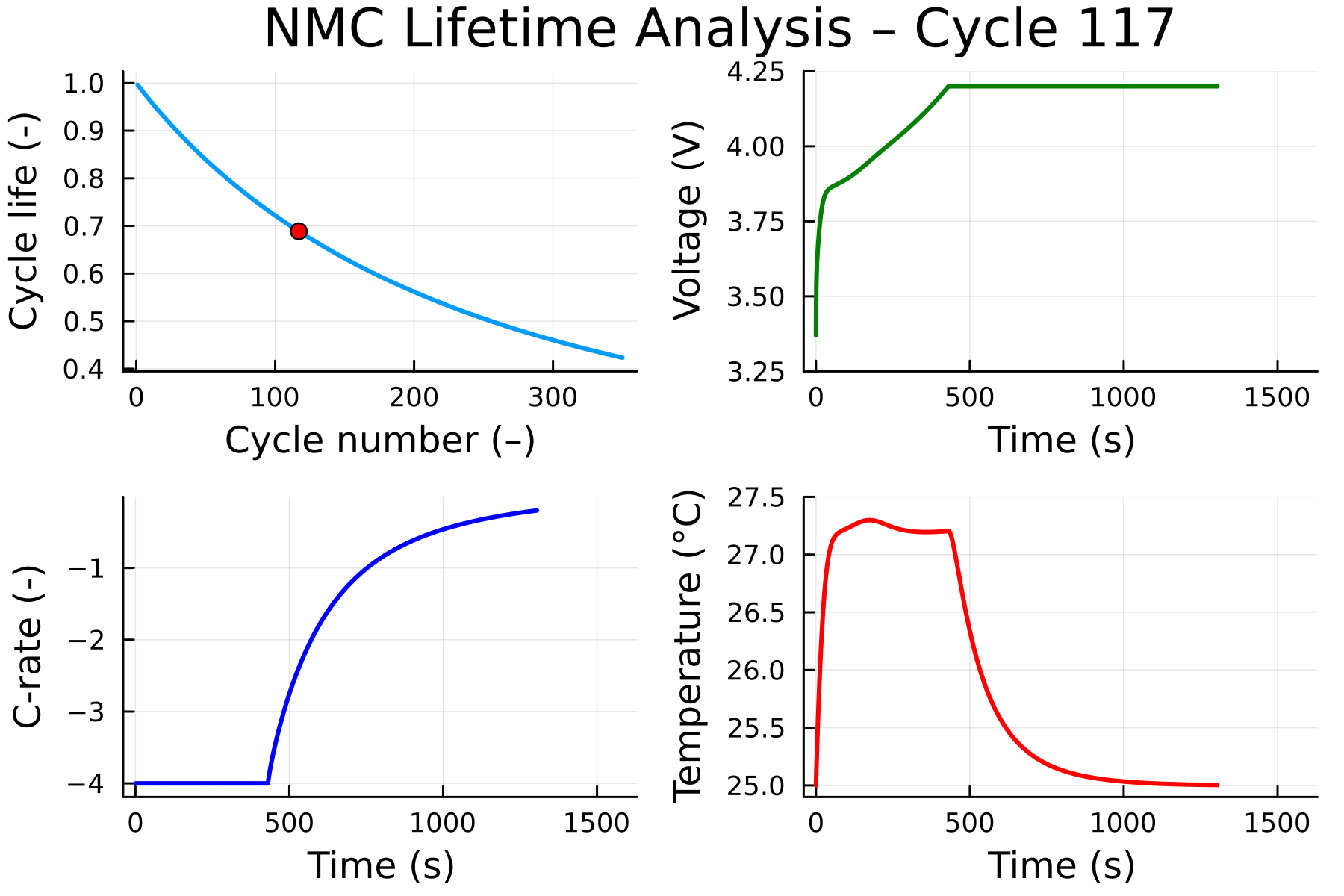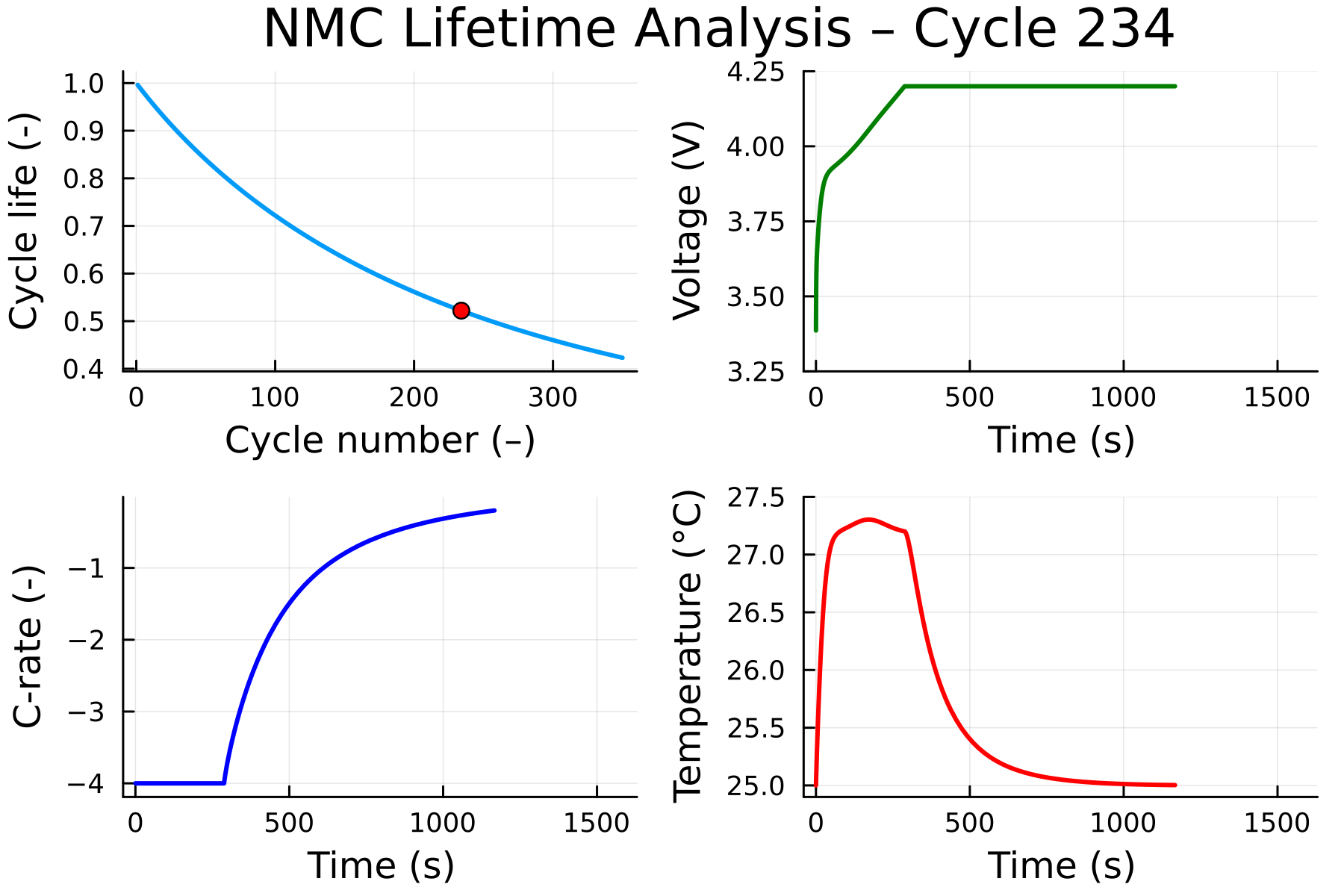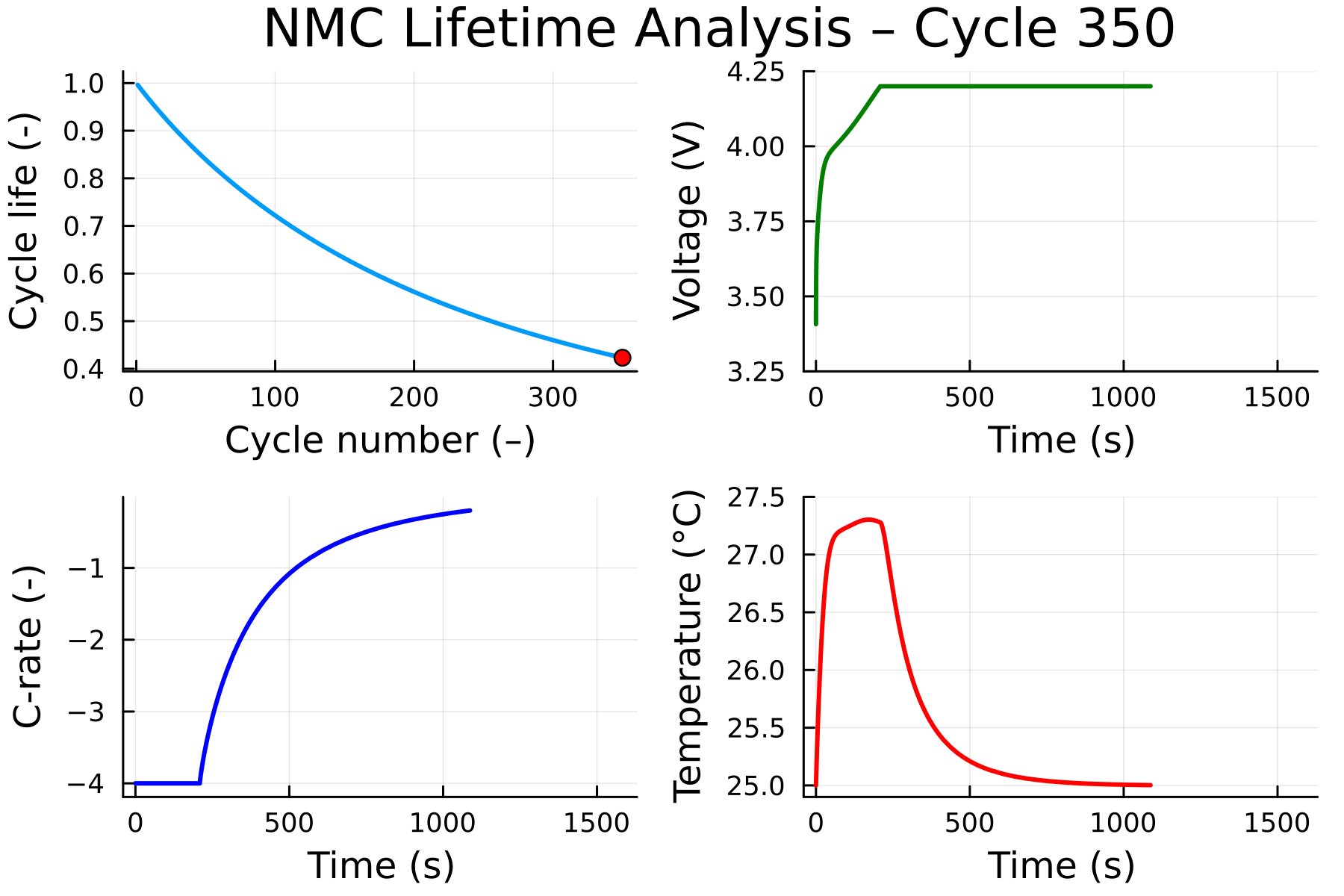
soh_cycle = sol["state of health"][last.(cycle_indices(sol))]
tspan = (0, sol.t[cycle_indices(sol; charge=true)[1][end]] / 3600)
@gif for cycle in 1:cycle_count
kwargs = (; cycle=cycle, charge=true, time_unit=u"hr", xlims=tspan,
width=3, legend=false, xwiden=1.06, ywiden=1.06)
## State of Health
plt1 = plot(1:cycle, 100(soh_cycle)[1:cycle];
xlabel = "cycle number (–)", ylabel="state of health (%)", kwargs...)
scatter!(plt1, [cycle], [100(soh_cycle)[cycle]]; color = :red)
xlims!(plt1, (1, cycle_count))
ylims!(plt1, 100 .*(soh_cycle[end], 1))
plt2 = plot(sol, "voltage";
color = :green, kwargs...)
plt3 = plot(sol, "C-rate";
kwargs...)
ylims!(plt3, (-4, 0))
plt4 = plot(sol, "cell-averaged temperature";
unit=u"°C", color = :red, kwargs...)
plot(plt1, plt2, plt3, plt4)
end